Йлесімдік орташа шама. 1.Орташа шаманың мәні және қолданылу шарттары

Лекция 8

1.Орташа шаманың мәні және қолданылу шарттары

2. Арифметикалық орташа шамалар

4. Мода және медиана

1. Орташа шаманың мәні және қолданылу шарттары

Орташа шама деп, біртектес жиынтықты белгілі бір жағдайда және белгілі бір уақытта өздеріне тән белгісі бойынша жинақтап көрсететін орташа сан мөлшерін, яғни біртектес жиынтық бірліктерінің ортақ есеппен алынатын белгісінің барлық бірліктерге жатқызылатын сандық шамасын айтады.

Статистикада орташа шаманы есептегенде және қолданғанда төменде берілген принциптер мен шарттар толықтай орындалуы тиіс: 1) зерттеп отырған құбылыстың, процестің жиынтық бірліктері біртекті болуы шарт; 2)орташа шаманы есептегенде оның жеке дара өзгермелі сандық және сапалық көрсеткіштері толығымен жойылады; 3) орташа шаманың көрсеткіші статистикалық бақылау нәтижесінде жиналған мәліметтер арқылы есептелінеді, бақылау көрсеткіштері неғұрлым көп болатын болса, соғұрлым орташа шама дұрыс шығады; 4) зерттеп отырған құбылыстар мен процестердің жеке бөліктерінің арасында ауытқу болатын жағдайларда орташа шама қолданылады.

Қоғамдық құбылыстардың өзара байланыстылығымен, өсіңкілігін немесе кемуін анықтауда, сонымен қатар стататистикалық бақылау, топтау, мәліметтерге талдау жасаудада орташа шама әдісі қолданылып, зерттелінеді.

Экономикалық зерттеулер мен жоспарлауларды есептеп анықтауда екі түрдегі орталар қолданылады: 1) дәрежелі орталар; 2) құрылымдық орталар.

Статистикада зерттеп отырған құбылыстар мен процестердің негізінде алдына қойған мақсатына және бастапқы берілген көрсеткіштердің мәніне сәйкес, дәрежелі орташа шамалардың бірнеше түрі қолданылады, олар мыналар: арифметикалық, геометрикалық, құрылымдық, үйлесімдік және шаршылық (квадраттық) орташа шамалар.[23]

2. Арифметикалық орташа шамалар

Арифметикалық орташа шама жалпы жиынтықтағы өзгермелі белгілердің жеке мәндерінің қосындысы болған жағдайда ғана қолданылады. Арифметикалық орташа шама біртектес бірлік көрсеткіштердің жеке мәндерінің мағынасына қарай жәй және салмақталған болып екі топқа бөлінеді.

Жиынтықта әрбір белгі тек бір рет қана кездессе, яғни бір-ақ рет қайталанса немесе барлық белгілердің (варианттардың) жиіліктері бірдей болса, онда арифметикалық орташаның жай түрі қолданылады. Ол өзгермелі белгілердің мәндерін бір- біріне қосып, одан шыққан қосындыны белгінің санына бөлгенге тең болып мына формула арқылы есептелінеді:

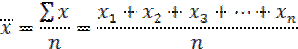
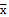- жай орташа арифметикалық шама

х – белгілердің жеке сандық мәндері;

n- белгілердің саны;

Σ – жиынтық белгісі, яғни х – тың қосындысы.

Мысалы, кәсіпорынның екінші бөлімінде бір жұмысшы орташа қанша тетік өндірді, егер бөлімдегі 14 жұмысшының әр қайсысының өндірген тетігі анық, яғни жеке (дара) белгілердің мәндерінің қатары төмендегідей берілген болса:

42, 38, 40, 42, 39, 40, 38, 42, 38, 39, 41, 39, 41, 42.

Арифметикалық орташаның жай түрі формула бойынша төмендегідей анықталады, дана:

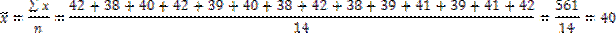
Егер жиынтықтың әрбір белгісі бір рет емес, бірнеше рет қайталанатын болса, яғни жиілік бірліктерінің саны берілген болса, онда арифметикалық орташа шаманың салмақталған түрі қолданылады. Оны есептеу үшін әрбір қатардағы белгі мәндерін х жиілілік көрсеткішіне f көбейтіп, одан шыққан көбейтінділердің қосындысын жиіліктің жалпы санына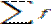

бөлеміз және ол мына формула арқылы өрнектеледі:

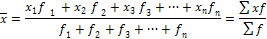
Мұнда

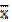- салмақталған орташа арифметикалық шама

х – белгілердің жеке сандық мәндері;

f – жиіліктің мәндері

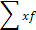– белгілер мен жиілік мәндерінің көбейтіндісінің қосындысы;

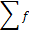– жиіліктің жалпы саны.

Арифметикалық орташа шаманың салмақталған түрінің есептеу техникасын жоғарыда мысал бойынша көрсетеміз. Ол үшін берілген мәліметті топтап, оны 1- кестеге төмендегідей жайғастырамыз.

Арифметикалық орташаның салмақталған түрі формула бойынша төмендегіге тең, дана

Кесте 1. і - Тетіктерді өндіру бойынша жүмысшыларды бөлу.

1 жұмысшының бір жұмыс күніндегі өндірген тетігі, дана, х	Жұмысшылар саны(жиілігі) f	xf
Барлығы

Арифметикалық орташаның салмақталған түрі формула бойынша төмендегіге тең, дана:

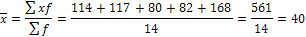
Сонымен, орташаның, негізгі қатынасы бөлімінің мәні белгілі де, алымының мәні белгісіз болған жағдайларда арифметикалық орташа шаманың салмақталған түрі қолданылады.[24]

Дата добавления: 2014-12-07