
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Часть I
|
|
|
|
Решение системы линейных уравнений по формулам Крамера
Рассмотрим систему уравнений:
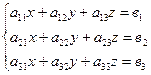 (1)
(1)
где х,у,z – неизвестные; коэффициенты а 11, а 12,…., а 33 и свободные члены 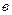 1,
1, 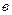 2,
2, 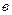 3 – известные постоянные (числа)
3 – известные постоянные (числа)
Введем обозначения:
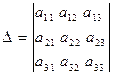 ;
; 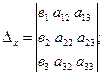
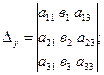
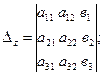
Определитель 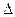 , составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
, составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Определители 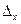 ,
, 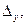
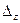 получаются из определителя
получаются из определителя 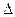 при помощи замены соответственно его первого, второго и третьего столбца – столбцом свободных членов данной системы.
при помощи замены соответственно его первого, второго и третьего столбца – столбцом свободных членов данной системы.
Если 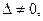 то система (1) имеет единственное решение; оно определяется формулами:
то система (1) имеет единственное решение; оно определяется формулами:

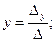
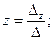 (2)
(2)
Формулы (2) называются формулами Крамера.
Если определитель системы 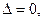 а хотя бы один из определителей
а хотя бы один из определителей 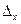 ,
, 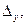
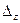 отличен от нуля, то система (1) не имеет решений.
отличен от нуля, то система (1) не имеет решений.
В случае, когда 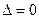 и одновременно
и одновременно 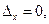
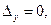
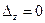 , система (1) также может не иметь решений; но если система в этом случае имеет хотя бы одно решение, то она имеет бесконечно много решений.
, система (1) также может не иметь решений; но если система в этом случае имеет хотя бы одно решение, то она имеет бесконечно много решений.
Решение типового примера.
Пусть требуется, используя формулы Крамера, решить систему
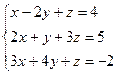
Вычислим сначала главный определитель системы 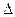 , воспользовавшись следующим правилом вычисления определителей третьего порядка:
, воспользовавшись следующим правилом вычисления определителей третьего порядка:
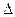 =
=  .
.
У нас
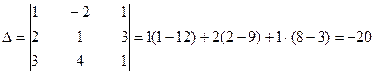
Так как 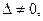 делаем вывод о том, что система имеет единственное решение. Найдём его. Вычислим вспомогательные определители
делаем вывод о том, что система имеет единственное решение. Найдём его. Вычислим вспомогательные определители 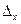 ,
, 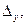
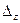 .
.
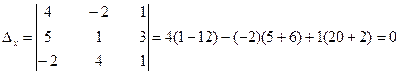 ;
;
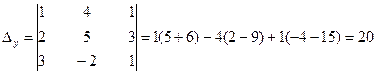 ;
;
 .
.
Далее, воспользовавшись формулами Крамера, окончательно получим
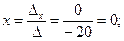
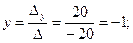
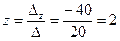 .
.
Осуществим проверку правильности полученного решения, подставив его в каждое уравнение заданной системы:
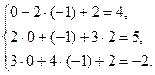
Все три равенства верные, поэтому делаем вывод о правильности полученного решения.
Ответ: х = 0; у = –1; z = 2.
Часть II
Матричный метод решения системы линейных уравнений.
Рассмотрим систему линейных уравнений
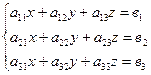 (1)
(1)
Обозначим через А – матрицу коэффициентов при неизвестных; X – матрицу – столбец неизвестных х, у, z; В – матрицу – столбец свободных членов 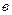 1,
1, 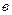 2,
2, 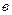 3:
3:
А = 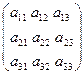 ; Х =
; Х = 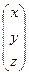 ; В =
; В = 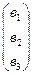
С учетом этих обозначений данная система уравнений (1) принимает следующую матричную форму:
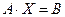 (2)
(2)
Если матрица А – невырожденная (ее определитель 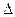 отличен от нуля), то она имеет обратную матрицу
отличен от нуля), то она имеет обратную матрицу 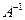 . Умножив обе части уравнения (2) на
. Умножив обе части уравнения (2) на 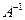 , получим:
, получим:
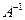
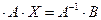 .
.
но 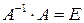 (Е – единичная матрица), а
(Е – единичная матрица), а 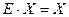 , поэтому
, поэтому
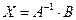 (3)
(3)
Равенство (3) называется матричной записью решения системы линейных уравнений (1). Для нахождения решения системы уравнений необходимо вычислить обратную матрицу 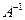 .
.
Пусть имеем невырожденную матрицу
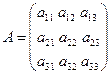 , ее определитель
, ее определитель 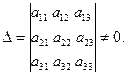
Тогда
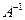 =
= 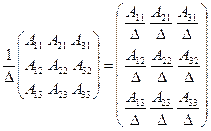 (4)
(4)
где А 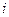 j (
j (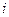 =1, 2, 3; j=1, 2. 3) – алгебраическое дополнение элемента
=1, 2, 3; j=1, 2. 3) – алгебраическое дополнение элемента 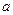 ij в определителе матрицы А, которое является произведением
ij в определителе матрицы А, которое является произведением 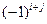 на минор (определитель второго порядка), полученный вычеркиванием
на минор (определитель второго порядка), полученный вычеркиванием 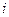 -ой строки и j-го столбца в определителе матрицы А.
-ой строки и j-го столбца в определителе матрицы А.
Решение типового примера.
Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы.
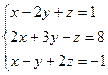
Обозначим матрицы
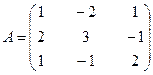 ; Х =
; Х = 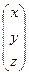 ; В =
; В = 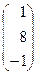 .
.
Тогда матричная форма записи данной системы будет
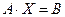 ,
,
или
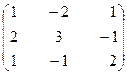
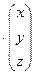 =
= 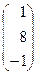
Найдем обратную матрицу 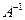 для матрицы А. Для этого:
для матрицы А. Для этого:
1) Вычислим определитель матрицы А.
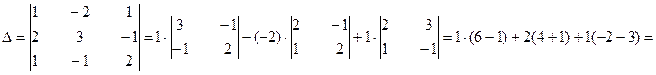
= 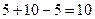
 Получили
Получили 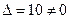 . Следовательно матрица А имеет обратную матрицу
. Следовательно матрица А имеет обратную матрицу 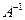 .
.
2) Найдем алгебраические дополнения для каждого элемента определителя 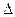 матрицы А.
матрицы А.
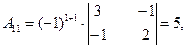
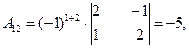
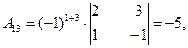
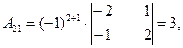
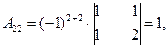


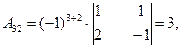
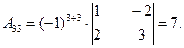
3) Обратная матрица 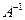 будет иметь вид:
будет иметь вид:
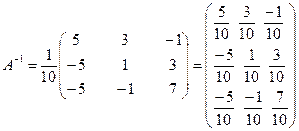
4) Проверим правильность полученной обратной матрицы (произведение обратной матрицы 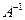 на матрицу А должно быть равно единичной матрице Е).
на матрицу А должно быть равно единичной матрице Е).
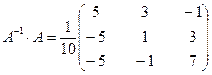
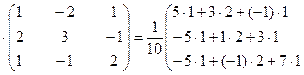
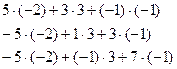
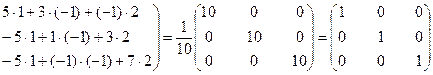
Получили единичную матрицу. Значит обратная матрица найдена верно.
Находим решение данной системы уравнений в матричной форме
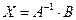
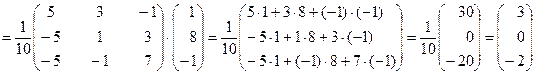
Получили 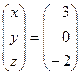 , следовательно х = 3; у = 0; z = –2.
, следовательно х = 3; у = 0; z = –2.
Проверим правильность полученного решения, подставив его в каждое уравнение заданной системы:
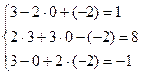
Все три равенства верные, поэтому делаем вывод о правильности полученного решения.
Ответ: х = 3, у = 0, z = –2
Часть III
Решение системы линейных уравнений методом Гаусса.
При решении системы линейных уравнений часто применяется метод Гаусса. Сущность этого метода поясним на примерах.
- Рассмотрим систему трех линейных уравнений с тремя неизвестными
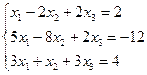
Решение.
Исключим из последних двух уравнений х1. Для этого умножим первое уравнение на -5 и результаты прибавим соответственно ко второму уравнению, затем обе части первого уравнения умножим на -3 и результаты прибавим к третьему уравнению. В результате получим систему, эквивалентную данной:

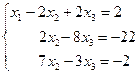 (1)
(1)
Разделив обе части второго уравнения системы (1) на 2, получим систему
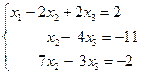 (2)
(2)
Теперь исключим из третьего уравнения системы (2) х2.
Для этого обе части второго уравнения этой системы умножим на — 7 и результаты прибавим к третьему уравнению. В результате получим систему
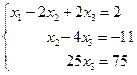 (3)
(3)
Откуда х3 =3, х2=1 и х1=–2. Это решение заданной системы
Приведение данной системы к ступенчатому виду (3) практически более удобно, если использовать преобразования расширенной матрицы данной системы, т. е. матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид
 .
.
Умножим элементы первой строки матрицы на — 5 и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на — 3 и результаты прибавим к элементам третьей строки. Получим матрицу
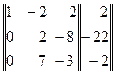 .
.
Разделив элементы второй строки на 2, получим
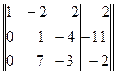 .
.
Элементы второй строки умножим на — 7 и результаты прибавим к элементам третьей строки. Получим матрицу
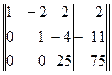 ,
,
которая позволяет данную систему привести к виду (3) и затем решить ее.
- Рассмотрим систему уравнений
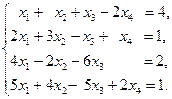
Решение. Составим расширенную матрицу системы:
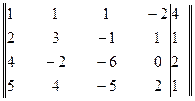
Умножим элементы первой строки последовательно на -2, -4 и -5. Полученные результаты прибавим соответственно к элементам второй, третьей и четвертой строкам. Получим матрицу
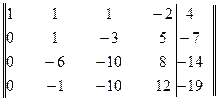
Элементы второй строки умножим на 6 и результаты прибавим к элементам третьей строки, затем элементы второй строки прибавим к элементам четвертой строки. Получим матрицу
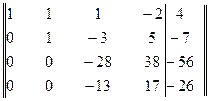
Элементы третьей строки разделим на -2 и затем элементы четвертой строки прибавим к элементам третьей строки. Получим матрицу

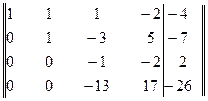
Теперь элементы третьей строки умножим на 13 и результаты прибавим к элементам четвертой строки. Получим матрицу
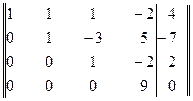
Следовательно, данную систему можно записать так:
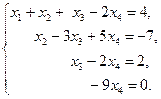
Откуда х4 =0, х3=2, х2=–1 и х1=–3.
Матрицы, получаемые после соответствующих преобразований, являются эквивалентами. Их принято соединять знаком ~.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 411; Нарушение авторских прав?; Мы поможем в написании вашей работы!