
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Часть III
|
|
|
|
Часть II
Часть I
Задачи для расчетной работы №2
В задачах 1-20 решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
1. 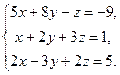 2.
2. 
3.  4.
4. 
5.  6.
6. 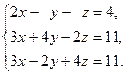
7. 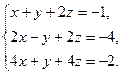 8.
8. 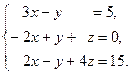
9.  10.
10. 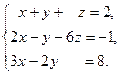
11. 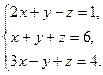 12.
12. 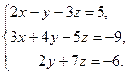
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 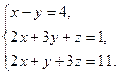
19.  20.
20. 
В задачах 1-20 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения
1.  2.
2. 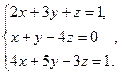
3. 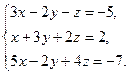 4.
4. 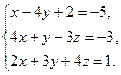
5. 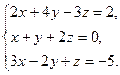 6.
6. 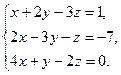
7.  8.
8. 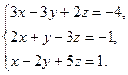
9. 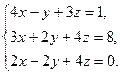 10.
10. 
11.  12.
12. 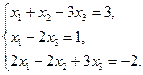
13.  14.
14. 
15.  16.
16. 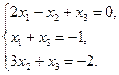
17.  18.
18. 
19.  20.
20. 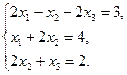
В задачах 1-10 решить данную систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 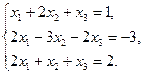
9.  10.
10. 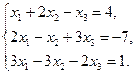
Задачи линейного программирования.
Графический метод.
Несмотря на то, что графический метод решения задач линейного программирования применяется только для задач с двумя искомыми переменными (или в случае трехмерного пространства с тремя), этот метод позволяет понять основную суть линейного программирования.
Задача 1.
Рассмотрим систему неравенств
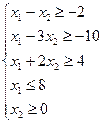 (1)
(1)
и линейную форму
 (2)
(2)
Найти минимум и максимум линейной формы (2) из области решений системы (1).
Решение.
Построим выпуклый многоугольник, заданный системой неравенств (1). Для этого построим прямоугольную систему координат х1ох2. Если в этой системе координат построить прямую ах1+bх2=с, то эта прямая разбивает плоскость х1ох2 на две полуплоскости, каждая из которых лежит по одну сторону от прямой. Сама прямая в этом случае называется граничной и принадлежит обеим полуплоскостям. Координаты точек, лежащих в одной полуплоскости удовлетворяют неравенству ах1+вх2≤с, а координаты точек, лежащих в другой полуплоскости, удовлетворяют неравенству ах1+вх2≥с. Построим в плоскости х1ох2 граничные прямые:
1)  4)
4) 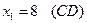
2) 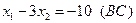 5)
5) 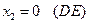
3) 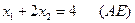
В результате получим пятиугольник АВСDЕ (рис. 2)
Значения х1 и х 2, удовлетворяющие системе неравенств (1), являются координатами точек, лежащих внутри или на границе найденного пятиугольника. Теперь задача сводится к тому, чтобы найти те значения х 1 и х 2 при которых линейная форма L (2) имеет минимум, и те значения х1 и х 2 при которых линейная форма L достигает максимума. Из рис. 2 видно, что координаты всех точек, лежащих внутри или на границе пятиугольника, не являются отрицательными, т.е. все значения х 1 и х 2 больше или равны нулю.
|

Для каждой точки плоскости х1ох 2 линейная форма L принимает фиксированное значение. Множество точек, при которых линейная форма L принимает фиксированное значение L 1, есть прямая 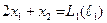 , которая перпендикулярна вектору
, которая перпендикулярна вектору 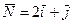 . Если прямую
. Если прямую 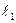 передвигать параллельно самой себе в положительном направлении вектора
передвигать параллельно самой себе в положительном направлении вектора 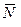 , то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую
, то линейная форма L будет возрастать, а в противоположном направлении – убывать. Построим прямую 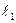 для того случая, когда L = 0, т.е. построим прямую
для того случая, когда L = 0, т.е. построим прямую 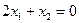 . Как видно из рис. 2, при передвижении прямой
. Как видно из рис. 2, при передвижении прямой 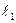 в положительном направлении вектора
в положительном направлении вектора 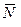 она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
она впервые встречается с вершиной А(0;2) построенного пятиугольника АВСDЕ. В этой вершине линейная форма L имеет минимум. Следовательно,
 .
.
При дальнейшем передвижении прямой 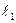 параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора 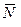 значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
значение линейной формы будет возрастать, и оно достигает максимального значения в точке С(8;6). Таким образом,
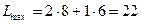 .
.
Задача 2.
Туристской фирме требуется не более 10 автобусов грузоподъёмностью 3 тонны и не более 8 автобусов грузоподъёмностью 5 тонн. Цена автобуса первой марки 20000 у.е., цена автобуса второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более 400000 у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной.
Решение.
Пусть приобретено х 1 трёхтонных, х 2 пятитонных автобусов, тогда заданные условия задачи можно записать так:
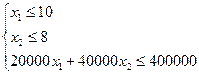 или
или  (1)
(1)
Линейная форма L (часто её называют целевой функцией) применительно к условиям нашей задачи имеет вид:
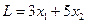 (2)
(2)
Требуется найти те значения х1 и х 2, при которых L достигает максимального значения. По условию задачи 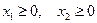 . Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
. Решим задачу графическим методом, который был использован при решении задачи 1. Построим многоугольник АВСDЕ (рис. 3), все точки которого удовлетворяют системе неравенств.
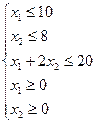 (3)
(3)
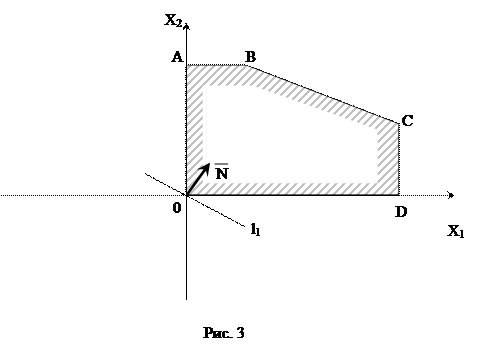

Затем построим вектор 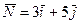 и прямую
и прямую  . Перемещая прямую
. Перемещая прямую  параллельно самой себе в положительном направлении вектора
параллельно самой себе в положительном направлении вектора  , установим, что L достигает максимального значения в точке С, для которой х 1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. (
, установим, что L достигает максимального значения в точке С, для которой х 1 = 10 и х2 = 5. Следовательно, туристской фирме следует приобрести 10 трёхтонных и 5 пятитонных автобусов. В этом случае общая грузоподъёмность составит 55 тонн. (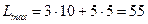 )
)
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 462; Нарушение авторских прав?; Мы поможем в написании вашей работы!