Понятие смешанной стратегии. Графический метод решения игры

Рассмотрим игру двух лиц с нулевой суммой:

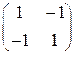
α = -1, β=1 → седловой точки нет!

Итак, гарантированный выигрыш игрока А составит -1. Можно ли его повысить?

Основатель теории игр фон Нейман предложил выбирать ходы случайным образом с определенными вероятностями. Набор этих вероятностей он назвал смешанной стратегией игрока (сумма вероятностей равна 1).

Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, как поведет себя противник в данной партии. Такая тактика (без всяких математических обоснований) часто применяется в карточных играх.

Тем самым, выигрыш игрока станет случайной величиной. Основная характеристика случайной величины – математическое ожидание (среднее). Итак, выигрыш это математическое ожидание.

(Напомним, что в теории вероятностей М (Х) = )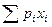

Пусть в нашем примере смешанная стратегия игрока А:

Р = (1/2, 1/2). Тогда, если, например, второй игрок В сделает первый ход, то математическое ожидание выигрыша игрока А:

1* (1/2) + (-1)*(1/2) = 0 → все же лучше, чем -1!.

Итак, случайность выбора ходов повышает шансы игрока на успех, хотя бы в среднем.

Фон Нейман обобщил это в виде теоремы.

Теорема фон Неймана

Существует такое число v (цена игры), что если игрок А придерживается оптимальной смешанной стратегии, то математическое ожидание его выигрыша (т.е. средний гарантированный выигрыш) будет не меньше v. Аналогичное утверждение относительно игрока В: математическое ожидание его проигрыша будет не больше v.

Как же найти цену игры v и оптимальные смешанные стратегии?

Графический метод

Дата добавления: 2014-12-27