Пример 1. Итак, игрок А выбрал 1-ю стратегию

Биматричные игры.

V - средний выигрыш

2 тур:

Итак, игрок А выбрал 1-ю стратегию. У игрока В накопленные проигрыши 4, 3, 3. Минимизируя свой проигрыш игрок В выберет 2-ю или 3-ю стратегию. Пусть ему приглянулась стратегия 3. Игрок А ответит либо 1, либо 2 стратегией. Его накопленные выигрыши либо 4, либо 3. Он ответит 1 стратегией, и т.д.

Вывод: после 10 туров v = 1,65. Игрок А воспользовался 1-й стратегией 3 раза- p₁ = 3/10= 0,30, 2- й стратегией 7 раз - р₂ = 7/10= 0,70.

Аналогично для игрока В: q₁ = 1/4, q₂=0, q₃ =2/3.

Как видно, всего после десяти итераций можно уже судить об основных тенденциях игры.

Выше мы рассмотрели игры с нулевой суммой, в которых интересы игроков прямо противоположны. Тогда оказалось достаточным иметь одну платежную матрицу.

Однако часто встречаются ситуации, в которых интересы двух игроков хотя и не совпадают, но не обязательно противоположны.

В этом случае получаются две платежные матрицы: одна матрица выплат игроку А, другая - матрица выплат игроку В. Подобную игру называют биматричной.

Класс биматричных игр значительно шире матричных игр.

Небольшая фирма А (игрок А) намерена сбыть партию товара на одном из двух рынков (две стратегии - выбор 1-го рынка, выбор 2-го рынка). Фирма В пытается воспрепятствовать этому, приняв предупредительные меры (например, демпинг) - также две стратегии- меры на 1-м рынке, меры на 2-м рынке.

Аналитики рассчитали две платежные матрицы:

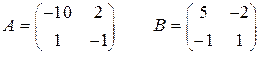
Видно, что, если оба игрока выберут один и тот же рынок, то победа за фирмой В. Если же фирмы уделят основное внимание разным рынкам, то победа за игроком А.

Как же найти оптимальные стратегии игроков?

Согласно теореме Нэша всякая биматричная игра имеет хотя бы одну равновесную ситуацию - когда игрокам невыгодно от нее отступать (тот же принцип, что и в § 12!).

Пусть (р, 1-р) – смешанная стратегия игрока А, (q, 1-q)- смешанная стратегия игрока В.

ПРАВИЛО:

1. с = а₁₁ + а₂₂ – (а₂₁ + а₁₂)

α = а₂₂ – а₁₂

2. Составить систему неравенств:

(р-1)(сq – α) ≥ 0

р (сq – α) ≥ 0 (1)

3. d = b₁₁ + b₂₂ – (b₂₁ + b₁₂)

β = b₂₂ – b₂₁

4. Составить систему неравенств:

(q-1)(dp – β) ≥ 0

q (dp – β) ≥ 0 (2)

5. Изобразив в системе координат ломаные линии, соответствующие решениям неравенств (1) и (2) найти точку их пересечения.

Для нашего примера будем иметь:

с= -10 -1 – (1+2)= -14

α = -1-2 = -3 p=1 → q ≤ 3/14

(р-1)(-14q + 3)) ≥ 0 p=0 → q ≥ 3/14

p (-14q +3)) ≥ 0 0 < p < 1 → q = 3/14

d= 5 + 1 – (-1-2)= 9

β = 2 q=1 → p ≥ 2/9

(q-1)(9p - 2)) ≥ 0 q=0 → p ≤ 2/9

q (9p - 2) ≥ 0 0 < q < 1 → p = 2/9

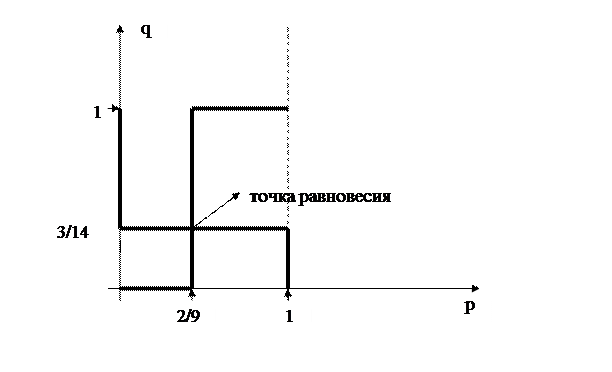
Рис. 8

Точка пересечения:

р = 2/9, 1-р = 7/9 – оптим. стратегия А

q=3/14, 1-q = 11/14 – оптим. стратегия В.

Рассчитаем средний выигрыш игрока А:

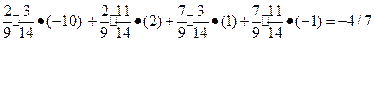
Для игрока В средний выигрыш 1/3.

Выводы:

Дата добавления: 2014-12-27