Работа. Мощность. Энергия

Изменение механического движения вызывают силы, действующие на тело. Если под действием силы тело проходит некоторый путь, то это означает, что совершается механическая работа.

Механическая работа – скалярная физическая величина, численно равная скалярному произведению вектора силы на вектор перемещения 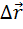. В процессе движения сила может оставаться постоянной и может изменяться.

Работа, совершаемая постоянной силой, на прямолинейной траектории:

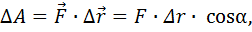(3.1)

где 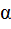– угол между направлением векторов силы и перемещения .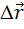

При движении по траектории произвольной формы элементарная работа, совершаемая постоянной силой, на участке 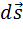(или ):

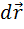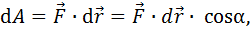(3.2)

где 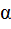– угол между направлением векторов силы и перемещения .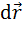

Интегрируя выражение (3.2) по всем элементарным участкам пути от точки 1 до точки 2, находим работу силы на конечном участке траектории:

(3.3)

где - проекция вектора силы на перемещение .

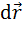Если сила постоянна и в декартовой системе координат равна 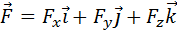, а перемещение равно 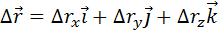, то с учетом правила скалярного произведения векторов интеграл (3.3) примет вид:

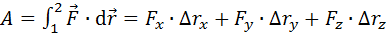, (3.4)

где 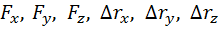- проекции вектора силы и вектора перемещения 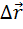на оси координат, соответственно.

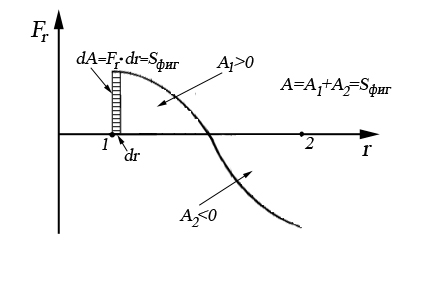
Выражение (3.3) имеет наглядное геометрическое представление. На рисунке представлена зависимость проекции силы 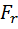от перемещения r. Элементарная работа равна площади заштрихованной полоски, а полная работа на пути от точки 1 до точки 2 равна площади фигуры, ограниченной кривой .

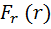Если сила является результирующей нескольких сил:

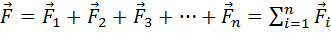,(3.5)

то работа результирующей силы аддитивна:

. (3.6)

Работа силы равна нулю в двух случаях:

· действующая сила перпендикулярна перемещению;

· тело движется по замкнутой траектории, то есть возвращается в исходное положение.

Для характеристики скорости совершения работы вводят понятие мощности.

Мощность – это работа, совершаемая в единицу времени.

Средняя мощность – работа, совершаемая за интервал времени :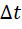

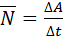. (3.7)

Мгновенная мощность – работа 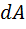, совершенная в данный момент времени 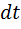(первая производная работы по времени):

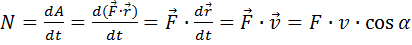, (3.8)

где 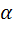– угол между вектором силы и вектором скорости .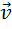

Коэффициент полезного действия (КПД) – величина, равная отношению полезной работы ко всей совершенной работе:

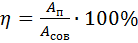. (3.9)

Коэффициент полезного действия не может быть больше единицы, так как неизбежны потери энергии, вызванные прежде всего работой силы трения.

Стационарное силовое поле, в котором работа сил поля на пути между двумя точками не зависит от формы пути, а зависит только от положения начальной и конечной точек, называют потенциальным (консервативным), а силы, действующие в нем – потенциальными (консервативными).

Если работа сил поля на любом замкнутом пути равна нулю, то поле является потенциальным.

Совершение работы приводит к изменению энергии – скалярной физической величины. В механике энергия может быть потенциальной и кинетической.

Потенциальная энергия – это энергия взаимодействия тел или частей одного и того же тела.

Потенциальная энергия тела, поднятого на высоту в однородном поле силы тяжести:

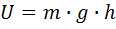. (3.10)

Потенциальная энергия упругой деформации тела:

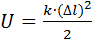, (3.11)

где 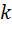– коэффициент жесткости тела,

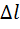- абсолютная деформация (изменение размеров тела).

Потенциальная энергия гравитационного взаимодействия двух тел:

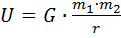, (3.12)

где 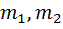– массы взаимодействующих тел,

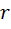– расстояние между телами,

G – гравитационная постоянная.

Потенциальная энергия тела в поле тяготения Земли на высоте h над уровнем:

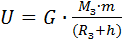, (3.13)

где 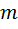– масса тела,

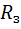– радиус Земли,

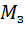– масса Земли,

G – гравитационная постоянная.

Работа консервативной силы на участке траектории от 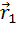до 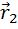не зависит от формы траектории и определяется разностью потенциальной энергии в начальной и конечной 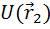точках (равна убыли потенциальной энергии):

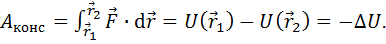(3.14)

Связь силы и потенциальной энергии :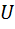

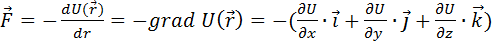, (3.15)

где 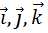– единичные векторы (орты),

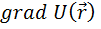– градиент потенциальной энергии,

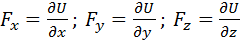– компоненты (проекции) вектора

силы.

Градиент – вектор, показывающий направление наиболее быстрого изменения скалярной величины вдоль нормали к поверхности уровня. Знак «-» в (3.14 – 3.15) указывает на то, что вектор силы и вектор градиента направлены в противоположные стороны.

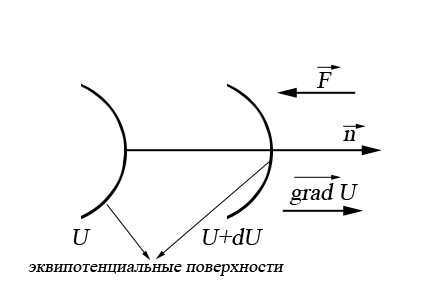
Работа консервативных сил (силы тяжести, силы упругости, силы тяготения):

· работа силы тяжести ;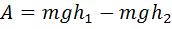

· работа силы упругости ;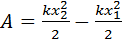

· работа силы тяготения .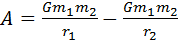

Кинетическая энергия – это энергия движущегося тела.

Для поступательного движения кинетическая энергия тела:

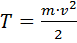. (3.16)

Теорема о кинетической энергии тела при поступательном движении:

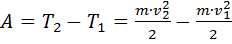. (3.17)

Работа неконсервативных сил (силы трения, силы сопротивления):

· работа силы трения .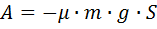

Полная механическая энергия тела равна сумме кинетической и потенциальной энергии тела:

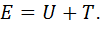(3.18)

Для изменения полной механической энергии необходимо совершить работу сторонними силами. При конечном перемещении тела приращение полной механической энергии тела равно работе сторонних сил:

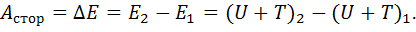(3.19)

В замкнутой системе сторонние силы отсутствуют и работа сторонних сил равна нулю:

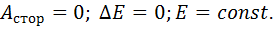(3.20)

Закон сохранения энергии: полная механическая энергия замкнутой (изолированной) системы тел, в которой действуют только консервативные силы, есть величина постоянная

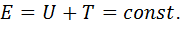(3.21)

В замкнутой системе приращение кинетической энергии равно убыли потенциальной энергии:

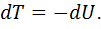(3.22)

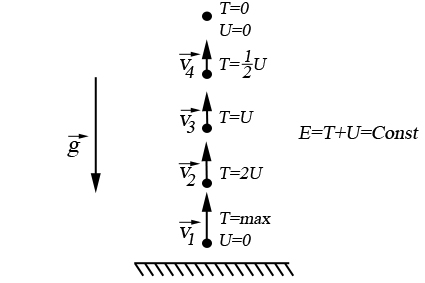
Пример выполнения закона сохранения (превращения) энергии.

Движение тела вертикально вверх.

Движение тела (скольжение или скатывание) с наклонной плоскости.

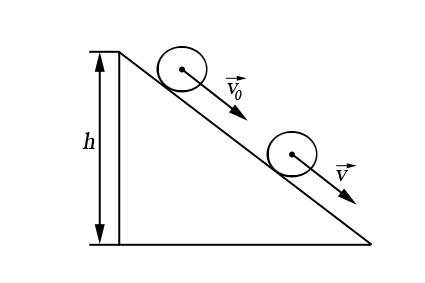
Тело скользит: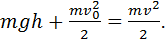

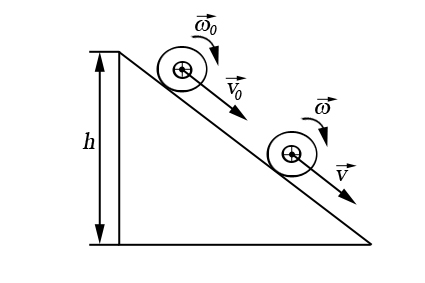
Тело скатывается: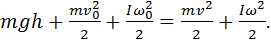

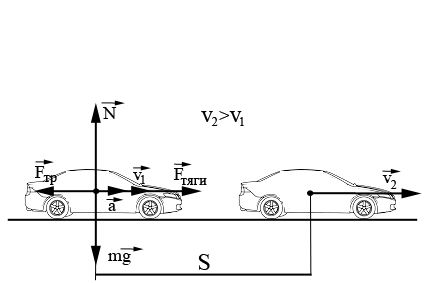
Движение автомобиля с ускорением

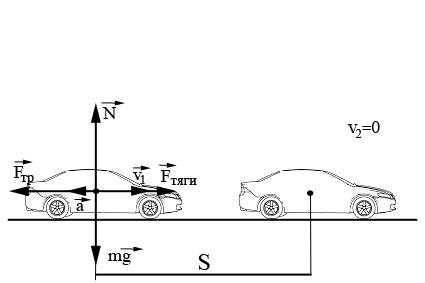
Торможение автомобиля

Дата добавления: 2014-12-27