
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Динамика вращательного движения
|
|
|
|
В разделе 1 (табл. 1) были обозначены характеристики вращательного движения.
Моментом силы 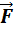 относительно полюса О называется вектор
относительно полюса О называется вектор 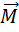 , равный векторному произведению радиус–вектора
, равный векторному произведению радиус–вектора 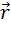 на вектор силы
на вектор силы  :
:
 (4.1)
(4.1)
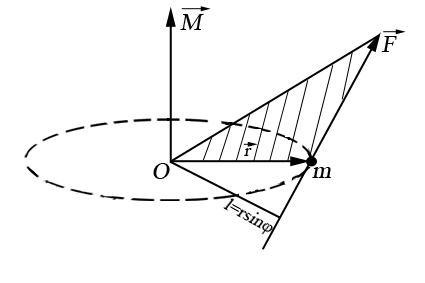
Вектор 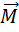 перпендикулярен к плоскости, содержащей векторы
перпендикулярен к плоскости, содержащей векторы 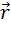 и
и  , а направление определяется по правилу правого винта.
, а направление определяется по правилу правого винта.
Правило правого винта: если ввинчивать винт так, чтобы направление вращения под действием силы совпало с направлением вращения материальной точки по окружности (при вращении от радиус-вектора к вектору силы по кратчайшему пути против часовой стрелки), то поступательное движение конца винта укажет направление вектора момента силы.
Абсолютная величина (модуль) вектора 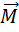 :
:
 , (4.2)
, (4.2)
где 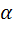 - угол между направлениями векторов
- угол между направлениями векторов 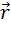
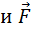 .
.
Произведение  называется плечом силы относительно точки О.
называется плечом силы относительно точки О.
Тогда абсолютная величина (модуль) вектора 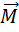 :
:
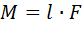 . (4.3)
. (4.3)
Моментом силы 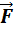 относительно неподвижной оси Z называется скалярная величина
относительно неподвижной оси Z называется скалярная величина  , равная проекции на эту ось вектора
, равная проекции на эту ось вектора 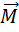 :
:
 (4.4)
(4.4)
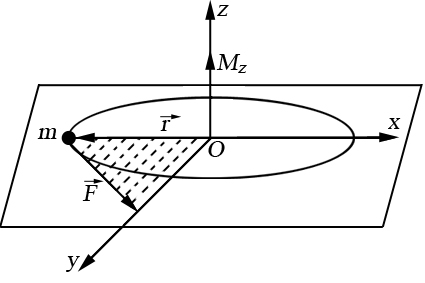
Вектор 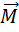 перпендикулярен к плоскости, содержащей векторы
перпендикулярен к плоскости, содержащей векторы 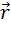 и
и  , а направление определяется по правилу правого винта.
, а направление определяется по правилу правого винта.
Правило правого винта: если ввинчивать винт так, чтобы направление вращения под действием силы совпало с направлением вращения материальной точки по окружности, то поступательное движение конца винта укажет направление вектора момента силы.
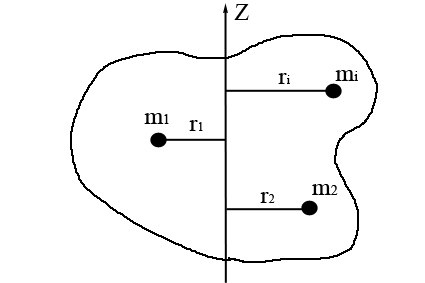
Моментом инерции материальной точки относительно полюса вращения О называется скалярная физическая величина I, численно равная произведению массы материальной точки на квадрат расстояния от нее до полюса вращения:
 (4.5)
(4.5)
Момент инерции является количественной характеристикой инерционных свойств точки (твердого тела).
Моментом инерции твердого тела относительно собственной оси вращения Z называется скалярная физическая величина I, численно равная алгебраической сумме моментов инерции всех материальных точек, составляющих твердое тело:
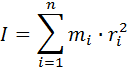
или
 (4.6)
(4.6)
где  – плотность тела,
– плотность тела,
dm – элементарная масса твердого тела,
V - объем твердого тела.
Собственной называется ось вращения, проходящая через центр масс (центр инерции) твердого тела.
Момент инерции зависит от:
· массы тела;
· размеров тела;
· формы тела;
· расстояния от тела до произвольной оси вращения.

Таблица 4 – Моменты инерции однородных твердых тел относительно оси симметрии, проходящей через их центр масс
| Тело | Ориентация оси | Момент инерции |
| Полый тонкостенный цилиндр | 
| 
|
| Кольцо | 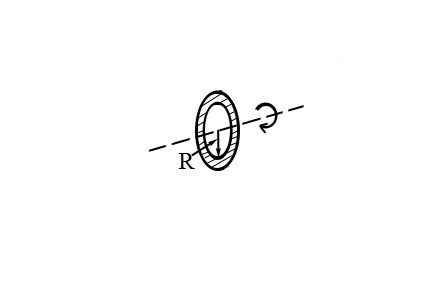
| |
| Сплошной цилиндр | 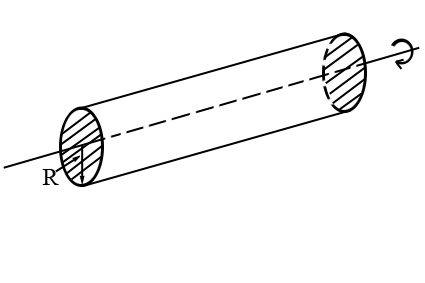
|

|
| Диск | 
| |
| Полый толстостенный цилиндр | 
| 
|
| Шар (полая тонкостенная сфера) | 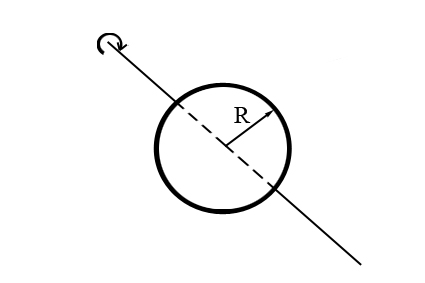
| 
|
| Шар (сплошная сфера) | 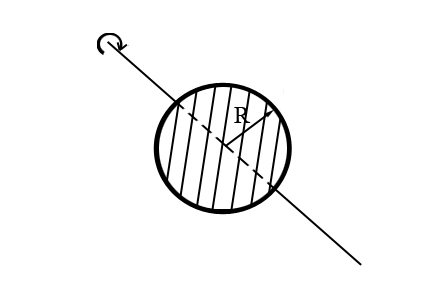
| 
|
| Тонкий стержень (ось проходит через центр масс и перпендикулярна ему) | 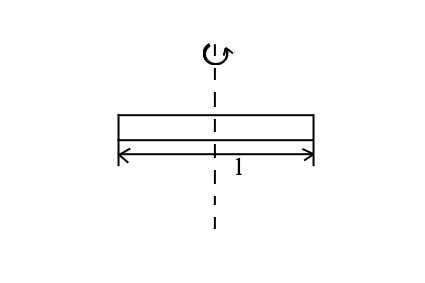
| 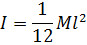
|
| Тонкий стержень (ось проходит через один из его концов и перпендикулярна ему) | 
| 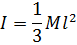
|
Если ось вращения не совпадает с собственной осью вращения твердого тела, то его момент инерции определяют по теореме Штейнера:
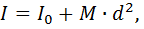 (4.7)
(4.7)
где  – момент инерции относительно собственной оси
– момент инерции относительно собственной оси
вращения,
M – масса твердого тела,
d – расстояние между собственной и произвольной осями
вращения,
 – произвольная ось вращения.
– произвольная ось вращения.
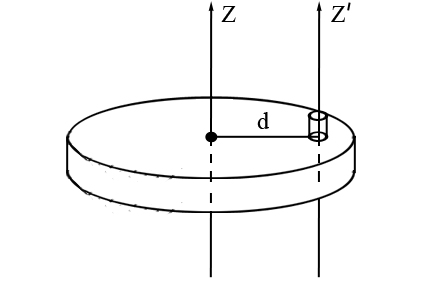
Теорема Штейнера: момент инерции твердого тела относительно произвольной оси вращения равен сумме момента инерции относительно собственной оси вращения, параллельной выбранной произвольной оси, и произведения массы твердого тела на квадрат расстояния между осями.
Моментом импульса материальной точки относительно полюса О называется вектор 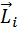 , равный векторному произведению радиус-вектора
, равный векторному произведению радиус-вектора  на вектор импульса
на вектор импульса  :
:
 (4.8)
(4.8)
 . (4.9)
. (4.9)
Вектор  перпендикулярен к плоскости, содержащей векторы
перпендикулярен к плоскости, содержащей векторы 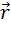 и
и  , а направление определяется по правилу правого винта.
, а направление определяется по правилу правого винта.
Правило правого винта: если ввинчивать винт так, чтобы направление вращения под действием силы совпало с направлением вращения материальной точки по окружности (при вращении от радиус–вектора к вектору импульса по кратчайшему пути против часовой стрелки), то поступательное движение конца винта укажет направление вектора момента импульса.
Моментом импульса твердого тела, состоящего из множества материальных точек, относительно оси вращения называется вектор  , равный векторной сумме моментов импульса
, равный векторной сумме моментов импульса 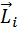 отдельных материальных точек:
отдельных материальных точек:
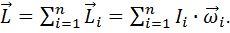 (4.10)
(4.10)
Учитывая, что все точки твердого тела вращаются с одинаковой угловой скоростью  , формула (4.10) примет вид:
, формула (4.10) примет вид:
 (4.11)
(4.11)
где I – момент инерции твердого тела,
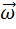 – вектор угловой скорости.
– вектор угловой скорости.
Вектор  перпендикулярен к плоскости, содержащей векторы
перпендикулярен к плоскости, содержащей векторы 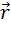 и
и  , а направление определяется по правилу правого винта.
, а направление определяется по правилу правого винта.
Правило правого винта: если ввинчивать винт так, чтобы направление вращения под действием силы совпало с направлением вращения материальной точки по окружности (при вращении от радиус–вектора к вектору импульса по кратчайшему пути против часовой стрелки), то поступательное движение конца винта укажет направление вектора момента импульса.
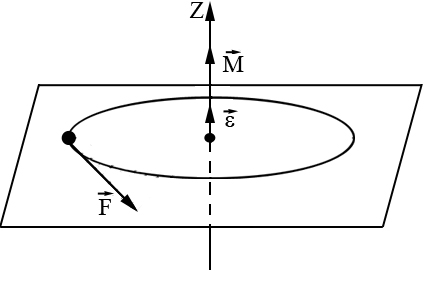
Основной закон динамики вращательного движения материальной точки (твердого тела) в интегральной форме: угловое ускорение вращения материальной точки (твердого тела) пропорционально моменту сил, действующих на точку (твердое тело) и обратно пропорционально моменту инерции точки (твердого тела):
 (4.12)
(4.12)

Основной закон динамики вращательного движения материальной точки (твердого тела) в дифференциальной форме: скорость изменения момента импульса твердого тела равна результирующему моменту сил, действующих на него:
 (4.13)
(4.13)
Разделяя переменные в (4.13), и переходя к интегрированию, получим закон изменения момента импульса:
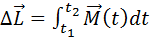 , (4.14)
, (4.14)
где  – импульс момента силы.
– импульс момента силы.
Таким образом, если точка (твердое тело) вращается под действием момента сил, изменяющимся по величине, изменение момента импульса за определенное время можно представить как интеграл, имеющий геометрический смысл площади криволинейной трапеции.
Если  , то (4.14) принимает вид:
, то (4.14) принимает вид:
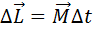 . (4.15)
. (4.15)
В замкнутой (изолированной) системе векторная сумма моментов сил равна нулю  , а внутренние моменты сил уравновешивают друг друга попарно, поэтому выполняется закон сохранения момента импульса:
, а внутренние моменты сил уравновешивают друг друга попарно, поэтому выполняется закон сохранения момента импульса:
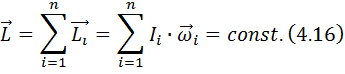
Закон сохранения момента импульса: в замкнутой (изолированной) системе полный момент импульса движения тел остается неизменным, какие бы изменения моментов импульса отдельных тел внутри системы не происходили.
Для тела, вращающегося около неподвижной оси, когда момент инерции тела меняется, закон сохранения момента импульса имеет вид:
 (4.17)
(4.17)
где  и
и  – начальное и конечное значения момента инерции
– начальное и конечное значения момента инерции
тела,
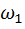 и
и 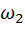 – начальное и конечное значения угловой скорости
– начальное и конечное значения угловой скорости
тела.
Элементарная работа, совершаемая моментом силы при повороте точки твердого тела на угол 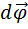 :
:
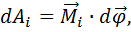 (4.18)
(4.18)
где 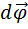 – вектор элементарного угла поворота тела.
– вектор элементарного угла поворота тела.
Полная работа, совершаемая моментом силы, при вращении твердого тела как системы материальных точек определяется из выражения:
 (4.19)
(4.19)
или
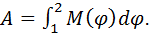 (4.20)
(4.20)
Если момент силы постоянный  , то работа момента силы равна:
, то работа момента силы равна:
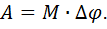 (4.21)
(4.21)
Кинетическая энергия тела, вращающегося относительно неподвижной оси:
 (4.22)
(4.22)
Теорема о кинетической энергии вращательного движения: работа, совершаемая моментом силы при вращательном движении твердого тела, равна приращению кинетической энергии вращательного движения твердого тела
 . (4.23)
. (4.23)
Если твердое тело одновременно участвует в поступательном и вращательном движениях, то его кинетическая энергия складывается из кинетической энергии поступательного и кинетической энергии вращательного движений
 . (4.24)
. (4.24)
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 8586; Нарушение авторских прав?; Мы поможем в написании вашей работы!