Кинематика поступательного и вращательного движения

Дополнительная

1. Андреев В.И. Педагогика. – Казань, 2000.

2. Афанасьев Ю.Н., Строголов А.С., Шеховцев С.Г. Об универсальном знании и новой образовательной среде. – М., 1999.

3. Зинченко В.П. Живое знание. – Самара, 1997.

4. Зинченко В.П.О целях и ценностях образования // Педагогика. – 1997. – № 5-6.

5. Ильин Е.Н. Искусство общения. – М., 1982.

6. Каптерев П.Ф. Педагогический процесс // Избр.пед.соч. – М., 1982.

7. Караковский В.А. Общечеловеческие ценности – основа целостного педагогического процесса. – М., 1993.

8. Касьян А.А. Гуманитаризация образования: некоторые теоретические предпосылки // Педагогика. – 1998. – №2.

9. Концепция модернизации российского образования // Вестник образования.—2002. – № 6.

10. Краевский В.В. Методология педагогического исследования. – Самара, 1994.

11. Кульневич С.В. Педагогика личности: от концепций до технологий. - Ростов н/Д., 2001

12. Курганов С.Ю. Ребенок и взрослый в учебном диалоге. – М., 1989.

13. Национальная доктрина образования // Учит.газ. – 2000. – № 42.

14. Никандров Н.Д. Ценности как основа целей воспитания // Педагогика. – №3.

15. Об образовании: Закон РФ. – М., 1996.

16. Об основных гарантиях прав ребенка в Российской Федерации: Закон РФ. – М., 1998.

17. Розов Н.С. Культура, ценности и развитие образования. – М., 1992.

18. Сенько Ю.В. Гуманитарные основы педагогического образования. - М., 2000.

19. Сенько Ю.В., Тамарин В.Э. Организация целостного процесса педагогического процесса в гимназии. – Барнаул, 1992.

20. Сериков В.В. Личностный подход в образовании: концепция и технологии. – Волгоград, 1994.

21. Сериков В.В. Личностно ориентированное образование. // Педагогика. – 1994. – №5.

22. Сластенин В.А., Мищенко А.И. Целостный педагогический процесс как объект профессиональной деятельности учителя. – М., 1999.

23. Сластенин В.А., Чижакова Г.И. Введение в педагогическую аксиологию. – М.,2003

24. Федеральная программа развития образования // Вестник образования. – 2000. – № 12.

Механическое движение тела – изменение положения тела в пространстве относительно других тел с течением времени.

Траектория – непрерывная линия, образованная множеством точек, через которые проходит материальная точка (тело) в данной системе отсчета.

Система отсчета – это совокупность тела, прибора для измерения времени и связанной с ними системы координат, относительно которой рассматривается движение материальной точки (тела) в течение некоторого интервала времени.

Перемещение – вектор 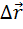, проведенный из начального положения точки в конечное (рис. 1).

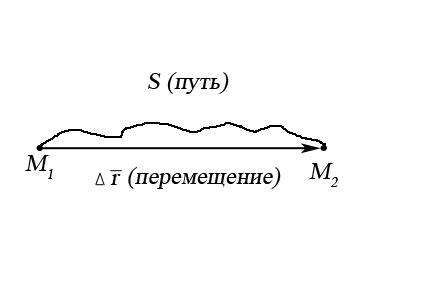
Рисунок 1 – Путь и перемещение тела

Путь – это расстояние S, пройденное телом (материальной точкой) за некоторое время по траектории движения.

Движение может быть:

- равномерным или неравномерным;

- прямолинейным или криволинейным;

- поступательным или вращательным.

Механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени, называется поступательным движением.

Характеристики поступательного движения представлены в таблице 1.

Таблица 1 – Характеристики движения

Характеристики поступательного движения тел	Характеристики вращательного движения тел
Линейное перемещение	Угловое перемещение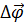
Линейная скорость	Угловая скорость
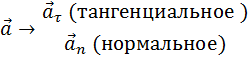
Линейное ускорение	Угловое ускорение
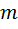
Масса	Момент инерции
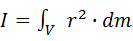
Сила	Момент силы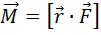
Уравнение движения тела	Уравнение движения тела
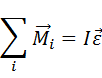
Импульс	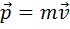Момент импульса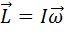
Работа	Работа
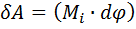
Кинетическая энергия тела	Кинетическая энергия тела

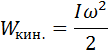
Положение материальной точки в пространстве в момент времени t определяется радиус-вектором :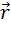

. (1.1)

Прямолинейным называется движениематериальной точки (тела) по прямолинейной траектории.

При прямолинейном движении модуль вектора перемещения равен пути:

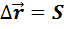, а во всех остальных случаях .

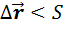Темп движения характеризуется скоростью – векторной физической величиной, численно равной отношению перемещения, совершенного точкой, к промежутку времени, за которое оно произошло:

. (1.2)

Проекции вектора скорости будут представлены уравнениями:

,

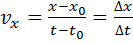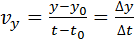, (1.3)

.

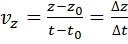Скорость движения материальной точки (тела) в данный момент времени или в данной точке траектории называется мгновенной скоростью, которая равна первой производной радиус-вектора по времени

(1.4)

или первой производной пути по времени

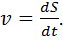(1.5)

Разделяя переменные в (1.4, 1.5), и переходя к интегрированию, получим векторный интеграл перемещения (или скалярный интеграл пути):

(1.6)

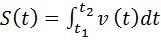. (1.7)

Таким образом, если точка движется со скоростью, изменяющейся постоянно по величине, перемещение (путь), совершенное (пройденный) точкой за определенное время можно представить как интеграл, имеющий геометрический смысл площади криволинейной трапеции.

Отношение перемещения точки к затраченному на это перемещение времени называется средней скоростью:

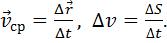(1.8)

Прямолинейным равномерным движением называют такое движение, при котором материальная точка (тело) за любые равные промежутки времени совершает одинаковые перемещения, т.е. движется с постоянной скоростью.

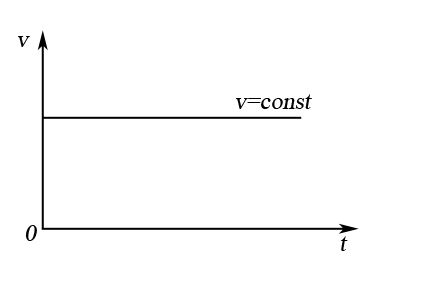
Графики зависимости пути и скорости от времени прямолинейного равномерного движения представлены на рисунке 2.

а) график пути

б) график скорости

Рисунок 2 – Графики зависимости скорости и пути от времени при прямолинейном равномерном движении

Прямолинейным неравномерным движением (равнопеременным) называют такое движение, при котором скорость за равные промежутки времени изменяется на одинаковую величину. Такое движение характеризуется ускорением.

Ускорение – векторная физическая величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло:

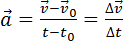. (1.9)

Проекции вектора ускорения будут представлены уравнениями:

,

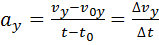, (1.10)

.

Мгновенным ускорением называется векторная физическая величина, численно равная первой производной скорости по времени или второй производной пути (перемещения) по времени:

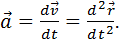(1.11)

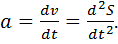(1.12)

Разделяя переменные в (1.11), и переходя к интегрированию, получим векторный интеграл скорости:

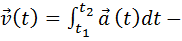векторный интеграл скорости.

Таким образом, если точка движется с ускорением, изменяющимся постоянно по величине, скорость можно представить как интеграл, имеющий геометрический смысл площади криволинейной трапеции.

Движение с постоянно возрастающей по модулю скоростью называют равноускоренным движением (, а с постоянно убывающей по модулю скоростью – равнозамедленным (. На рисунке 3 представлены графики пути, скорости и ускорения от времени для равнопеременного движения.

а) график пути

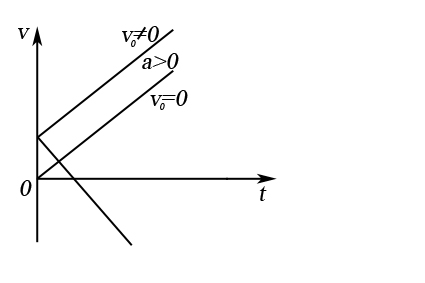б) график скорости

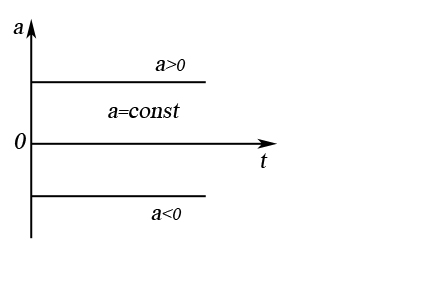в) график ускорения

Рисунок 3 – Графики зависимости пути, скорости и ускорения от времени для равнопеременного движения

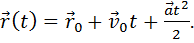(1.13)

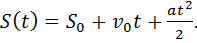(1.14)

Проекции (1.13) на оси координат принимают вид:

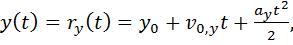(1.15)

Скорость точки при равнопеременном движении ()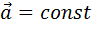

() (1.16) проекции (1.16) на оси координат принимают вид:

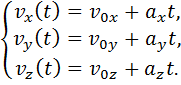(1.17)

В зависимости от величин тангенциального и нормального ускорений движения можно классифицировать:

1) равномерное прямолинейное движение:

2) равнопеременное прямолинейное движение:

2.1) равноускоренное

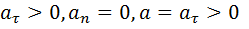
2.2) равнозамедленное

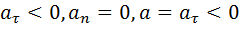
3) равномерное криволинейное движение:

4) равнопеременное криволинейное движение:

4.1) равноускоренное

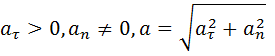
4.2) равнозамедленное

Вращательное движение – это такое механическое движение, при котором все точки твердого тела движутся по концентрическим окружностям, центры которых лежат на прямой, называемой осью вращения.

Характеристики вращательного движения представлены в таблице 1.

Угловое перемещение – это векторная физическая величина, модуль которой равен углу поворота радиус-вектора точки, а направление определяется по правилу правого винта («буравчика»).

Правило правого винта: если ввинчивать винт так, чтобы направление вращения совпало с направлением вращения материальной точки по окружности, то поступательное движение конца винта укажет направление вектора углового перемещения.

Угловая скорость – векторная физическая величина, характеризующая быстроту изменения углового перемещения материальной точки, а направление определяется по правилу правого винта («буравчика»).

Правило правого винта: если ввинчивать винт так, чтобы направление вращения совпало с направлением вращения материальной точки по окружности, то поступательное движение конца винта укажет направление вектора угловой скорости.

Мгновенная угловая скорость точки равна первой производной угла поворота точки по времени:

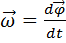. (1.18)

Средняя угловая скорость равна отношению углового перемещения точки к промежутку времени, за которое оно произошло:

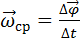. (1.19)

Разделяя переменные в (1.18), и переходя к интегрированию, получим векторный интеграл углового перемещения:

(1.20)

Таким образом, если точка вращается со скоростью, изменяющейся постоянно по величине, то ее угловое перемещение за определенное время можно представить как интеграл, имеющий геометрический смысл площади криволинейной трапеции.

Проекция векторного интеграла углового перемещения на ось вращения имеет вид:

. (1.21)

Угловое ускорение – векторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки, а направление определяется по правилу правого винта («буравчика»).

Мгновенное угловое ускорение точки равно первой производной угловой скорости точки по времени или второй производной углового перемещения по времени:

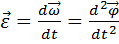. (1.22)

Среднее угловое ускорение равно отношению изменения угловой скорости точки к промежутку времени, за которое оно произошло:

. (1.23)

Разделяя переменные в (1.22), и переходя к интегрированию, получим векторный интеграл угловой скорости:

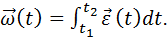(1.24)

Таким образом, если точка вращается с ускорением, изменяющимся по величине, то ее угловую скорость можно представить как интеграл, имеющий геометрический смысл площади криволинейной трапеции.

Проекция векторного интеграла угловой скорости на ось вращения имеет вид:

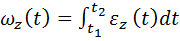. (1.25)

Вращение с постоянно возрастающей по модулю скоростью называют равноускоренным вращением (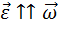), а с постоянно убывающей по модулю скоростью – равнозамедленным ( 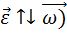(рис.4).

а) равноускоренное вращение

б) равнозамедленное вращение

Рисунок 4 – Направление векторных характеристик равноускоренного и равнозамедленного вращения

В таблице 2 приведены уравнения кинематики прямолинейного и криволинейного движения.

Таблица 2

Прямолинейное движение	Криволинейное движение
Равномерное движение	Равномерное вращение
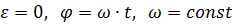
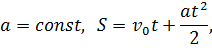
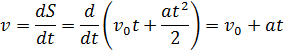
Равноускоренное движение	Равноускоренное вращение
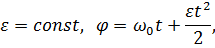
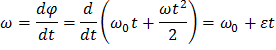
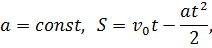
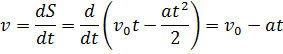
Равнозамедленное движение	Равноускоренное вращение

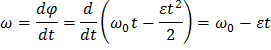
Частота вращения – число оборотов точки в единицу времени:

. (1.26)

Период вращения – время одного полного оборота точки:

(1.27)

Связь кинематических характеристик поступательного и вращательного движения:

- путь, пройденный точкой по дуге окружности радиусом R:

- угловая скорость:

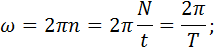
- линейная скорость точки:

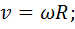
- тангенциальное ускорение:

- нормальное ускорение:

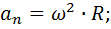
- полное ускорение:

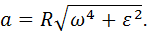
Дата добавления: 2014-12-27