
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Характеристики качества критерия
|
|
|
|
Общая логическая схема статистического
критерия
В целях проверки нулевой гипотезы в рассмотрение вводят специально подобранную случайную величину, распределение которой известно. Её обозначают U или Z, если она распределена нормально, F или 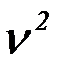 , если она распределена по закону Фишера-Снедекора, T – если по закону Стьюдента,
, если она распределена по закону Фишера-Снедекора, T – если по закону Стьюдента,  – если по закону хи-квадрат. Для общности её можно обозначить буквой K.
– если по закону хи-квадрат. Для общности её можно обозначить буквой K.
Определение: С лучайная величина K, которая служит для проверки нулевой гипотезы, называется статическим критерием.
Для проверки гипотезы сначала по данным выборки вычисляют значения входящих в критерий величин, а затем и сам критерий.
Определение: Вычисленное по выборкам значение критерия называют наблюдаемым значением и обозначают 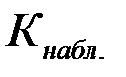 .
.
Область возможных значений критерия разбивают на две области: в одной находятся те значения, при которых гипотеза принимается, а в другой – те, при которых гипотеза отвергается.
Определение: Критической областью называется область значений критерия, при которых нулевая гипотеза отвергается.
Определение: Областью принятия гипотезы называется совокупность значений критерия, при которых гипотеза принимается.
Определение: Критическими точками (границами) 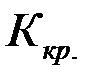 называются точки, отделяющие критическую область от области принятия гипотезы.
называются точки, отделяющие критическую область от области принятия гипотезы.
Определение: Правосторонней областью называется область, которая определяется неравенством 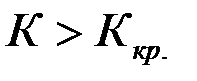 . Левосторонней областью называется область, которая определяется неравенством
. Левосторонней областью называется область, которая определяется неравенством 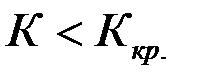 .
.
Двусторонние области определяются неравенствами  ,
, 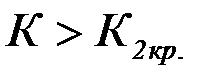 где
где  (
( 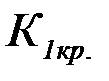 ,
, 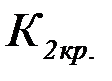 – критические точки).
– критические точки).
Для отыскания правосторонней критической области необходимо найти критическую точку исходя из условия:
P(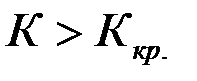 ) = α,
) = α,
где α – уровень значимости критерия.
Для отыскания левосторонней критической области необходимо найти критическую точку исходя из условия:
P(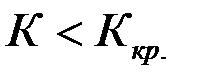 ) = α.
) = α.
Для отыскания двусторонней критической области необходимо найти критические точки исходя из условия:
Р( ) + Р(
) + Р(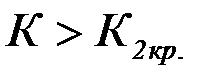 ) = α. (1)
) = α. (1)
Ясно, что критические точки могут быть выбраны бесчисленным множеством способов. Если же распределение критерия симметрично относительно нуля, и имеются основания выбрать симметричные относительно нуля точки  , и
, и 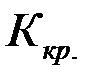 (
( ), то Р(
), то Р( ) = Р(
) = Р( ).
).
Учитывая формулу (1), получим Р(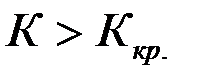 ) =
) = 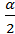 .
.
Это соотношение и служит для отыскания критических точек двусторонней критической области.
Для каждого критерия, т. е. соответствующего распределения, обычно составлены таблицы, по которым находят Kкр ..
После того, как критическая точка найдена, по данным выборки вычисляют наблюдаемое значение критерия.
Если 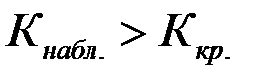 , то гипотезу
, то гипотезу  отвергают, если наоборот, то принимают.
отвергают, если наоборот, то принимают.
Определение: Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива альтернативная гипотеза.
Другими словами, мощность критерия – это вероятность того, что нулевая гипотеза будет отвергнута, если верна альтернативная гипотеза.
Пусть для проверки гипотезы принят определенный уровень значимости критерия α и выборка имеет фиксированный объем.
Остается произвол в выборе критической области. Покажем, что её целесообразно построить так, чтобы мощность критерия была максимальной.
Предварительно убедимся, что если вероятность ошибки второго рода (принять неправильную гипотезу) равна β, то мощность равна (1 – β).
Действительно, если β – вероятность события «принята нулевая гипотеза, причем справедлива альтернативная гипотеза», то мощность критерия равна (1 – β).
Пусть мощность (1 – β) возрастает. Тогда уменьшается вероятность β совершить ошибку второго рода. Таким образом, чем мощность больше, тем вероятность ошибки второго рода меньше.
Вывод: Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода.
Мощность критерия – это вероятность того, что не будет допущена ошибка второго рода.
Заметим, что чем меньше вероятность ошибок 1-го и 2-го рода, тем критическая область «лучше». Однако, при заданном объеме выборки уменьшить одновременно α и β невозможно. Если уменьшить α, то β будет возрастать. Следует выбирать α в зависимости от «тяжести последствий» ошибок для каждой конкретной задачи. Например, если ошибка 1-го рода повлечёт большие потери, а 2-го рода – малые, то следует выбрать возможно меньшее α.
Если α уже выбрано, то можно построить критическую область, для которой β будет минимальным и, следовательно, мощность критерия будет максимальной.
Единственный способ одновременного уменьшения вероятности ошибок 1-го и 2-го рода состоит в увеличении объема выборки.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 677; Нарушение авторских прав?; Мы поможем в написании вашей работы!