Данных

Пример обработки массива статистических

Дано статистическое распределение:

X
ni
X
ni
X
ni
X
ni

∑ = 60

Найдем размах выборки:

R = 582 – 537 = 45.

Переходим к интервальному ряду. Составим 8 или 9 частичных интервалов. Так как задано количество интервалов, то нет смысла применять общую формулу для нахождения длины частичного интервала h, просто поделим размах выборки на предполагаемое количество интервалов:

,

Выберем целочисленное значение длины интервалов h = 5, при этом получится 9 интервалов.

Построим интервальный ряд:

X	[537; 542)	(542;547]	(547; 552]	(552; 557]	(557; 562]
ni
X	(562; 567]	(567;572]	(572; 577]	(577; 582]
ni

Построим гистограмму относительных частот, используя формулу:

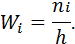
Вычислим середины интервалов по формуле

и перейдем от интервального ряда к точечному ряду:

	539,5	544,5	549,5	554,5	559,5	564,5	569,5	574,5	579,5
ni
Wi

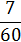
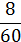
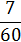
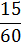
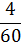
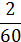
Построим полигон относительных частот.

Найдем эмпирическую функцию распределения (x) и построим ее график.

0 539,5 544,5 549,5 554,5 559,5 564,5 569,5 574,5 579,5 x

Найдем выборочные характеристики:

;

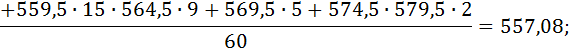
Дисперсию вычислим по формуле:

.

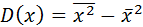= 310448,92 -

.

Проверим гипотезу о нормальном распределении по критерию Пирсона 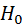: генеральная совокупность распределена нормально.

Альтернативная гипотеза : Генеральная совокупность не распределена нормально.

Составим расчетную таблицу.

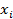
				Ф()	Ф()		’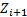
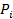
		-∞	-1,43	-0,5	-0,4236	0,0764	4,584	0,173	0,038
		-1,43	-0,96	-0,4236	-0,3315	0,0921	5,526	2,173	0,393
		-0,96	-0,48	-0,3315	-0,1844	0,1471	8,826	0,682	0,077
		-0,48	-0,01	-0,1844	-0,004	0,1804	10,824	14,623	1,351
		-0,01	0,47	-0,004	0,1808	0,1848	11,088	15,304	1,38
		0,47	0,94	0,1808	0,3264	0,1456	8,736	0,069	0,008
		0,94	1,42	0,3264	0,4222	0,0958	5,784	7,552	1,314
		1,42	1,89	0,4222	0,4706	0,0484	2,904	1,201	0,414
		1,89	+∞	0,4706	0,5	0,0294	1,764	0,56	0,032
	-	-	-	-	-			-	5,01

На одном графике с полигоном относительной частоты построим многоугольник распределения по точкам (, ).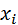

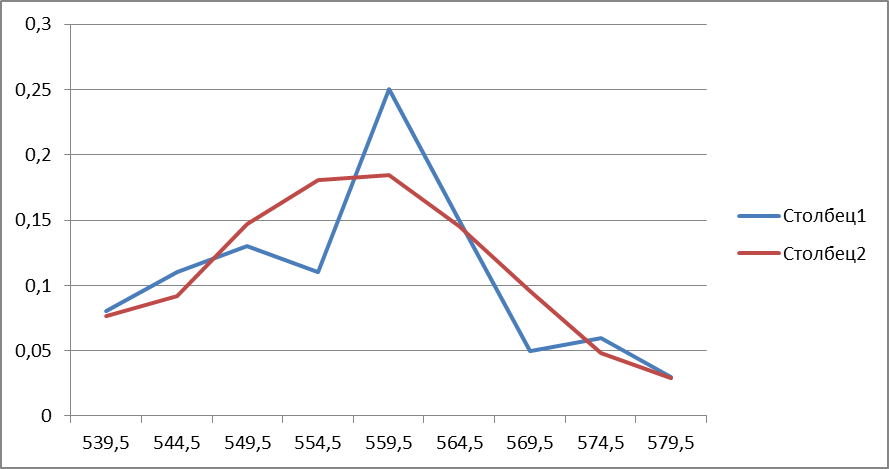
Наблюдаемое значение 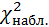= 5,01. По таблице критических точек распределения 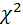найдем критическое значение 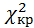, зависящее от уровня значимости критерия α и от k.

Пусть α = 0,05, а k = S – 3 = 9 – 3 = 6, где S – количество интервалов.

(0,05; 6) = 12,6.

<

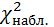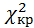
Вывод: Нет оснований отвергнуть нулевую гипотезу о нормальном распределении генеральной совокупности.

Вычислим доверительный интервал для оценки математического ожидания нормального распределения.

Пусть задана надежность .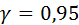

По таблице значений функции Лапласа находим t = 1,96.

Для вычисления доверительного интервала используем формулу:

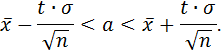
Тогда

557,08 - 2,66 < 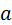< 557,08 + 2,66

Итак, получаем доверительный интервал:

(554,41; 559,74).

Дата добавления: 2014-12-27