Неравенство информации

Определение: Теорией информации называется наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации.

Черты случайности, присущие процессам передачи информации заставляют обратиться при изучении этих процессов к вероятностным и статистическим методам.

Определение: В математической статистике неравенством Краме́ра — Ра́о (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая её через информацию Фишера.

Определение: В математической статистике и теории информации информа́цией Фи́шера называется дисперсия функции вклада выборки.

Эта функция названа в честь описавшего её Рональда Фишера.

Пусть дана статистическая модель 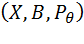, 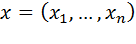— выборка размера n, определена функция правдоподобия и выполнены следующие условия (условия регулярности):

· L > 0 и везде дифференцируема по ;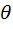

· Функция 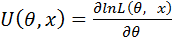(функция вклада выборки) имеет конечную дисперсию (или, что то же самое, конечна информация Фишера).

· Для любой статистики 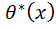имеет место равенство .

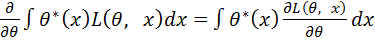Пусть при этих условиях дана статистика 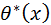, которая оценивает дифференцируемую функцию 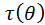, причём смещение 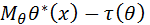равно дифференцируемой функции 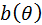. Тогда справедливы следующие утверждения:

· ;

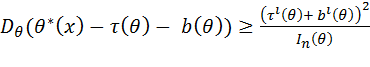· равенство достигается тогда и только тогда, когда 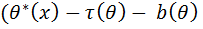представляется в виде .

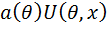Здесь 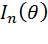— информация Фишера.

Часто используется следующая, более слабая версия неравенства. Пусть выполнены условия регулярности, а 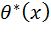— несмещённая оценка параметра 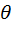. Тогда неравенство выглядит так:

.

Этот случай получается из первого, если взять 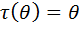и .

Заметим, что оценка параметра называется эффективной, если для неё неравенство Крамера — Рао обращается в равенство. Таким образом, неравенство может быть использовано для доказательства того, что диcперсия данной оценки наименьшая из возможных, то есть, что данная оценка в некотором смысле лучше всех остальных.

Определение: Пусть 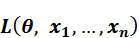— функция правдоподобия для данной статистической модели. Тогда если определена функция

,

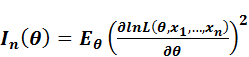где 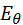— математическое ожидание при данном , то она называется информацией Фишера для данной статистической модели при n независимых испытаниях.

Поскольку математическое ожидание функции вклада выборки равно нулю, выписанная величина равна её дисперсии.

Если выборка состоит из одного элемента, то информация Фишера записывается так:

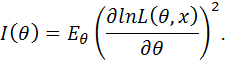
Из того, что в случае независимости случайных величин дисперсия суммы равна сумме дисперсий следует, что в случае n независимых испытаний .

Из указанного выше свойства дисперсий следует, что в случае независимости случайных величин 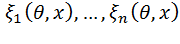(рассматриваемых в одной статистической модели) информация Фишера их суммы равна сумме информаций Фишера каждой из них.

Обозначим информацию Фишера для случайной величины 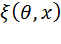через 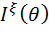. Если T() — статистика, для которой определена информация Фишера, то .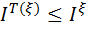

Дата добавления: 2014-12-27