Регрессионный анализ

Основы статистического исследования зависимостей.

Исследованием зависимостей занимаются такие разделы математической статистики, как регрессионный анализ и дисперсионный анализ. Рассмотрим эти разделы.

Многие экономические задачи требуют установить и оценить зависимость двух или более двух случайных величин. Эта зависимость может быть функциональной, статистической или совсем отсутствовать.

Отсутствие связи характерно для независимых случайных величин.

Определение: Если каждому значению случайной величины Х соответствует вполне определенное значение случайной величины Y, то говорят, что Х и Y связаны функциональной зависимостью.

Эта зависимость реализуется редко, т.к. обе величины подвержены действию случайных факторов.

Определение: Если каждому значению случайной величины Х соответствует вполне определенный закон распределения случайной величины Y, то говорят, что Х и Y имеет статистическую зависимость.

Частным случаем статистической зависимости является корреляционная зависимость, когда при изменении одной из величин изменяется среднее значение другой.

Определение: Если при изменении случайной величины Х меняется функция распределения вероятностей случайной величины Y, то говорят, что Х и Y имеют стохастическую зависимость.

На практике часто используется связь между изменениями одной случайной величины Х и изменениями математического ожидания другой случайной величины Y, т. е. регрессия Y на Х (условное математическое ожидание):

M(Y/X = x) = f(x)

или регрессия Х на Y:

M(X / Y = y) = f(y).

Так как в математической статистике имеют дело не с числовыми характеристиками законов распределения, а с их оценками, то в качестве оценки условного математического ожидания принимается условная средняя.

Определение: Условной средней 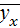называется среднее арифметическое наблюдаемых значений Y, соответствующих значению Х = х.

Пример: Если при Х = 2 случайная величина Y принимает значения 3, 6, 12, то условная средняя равна:

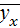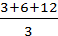= = 7.

Условные средние 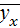и 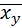являются функциями соответственно от х и y:

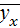= f*(х) (1),

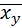= φ*(y) (2).

Уравнение (1) называется выборочным уравнением регрессии Y на X, а уравнение (2) – выборочным уравнением регрессии X на Y.

Графики соответствующих функций f*(x) и φ*(y) называются выборочными линиями регрессии.

Для данного значения Х = х наблюдается рассеяние Y около среднего значения 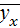. Мерой этого рассеяния служит условная дисперсия Y при данном значении х, обозначаемая .

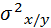Дата добавления: 2014-12-27