Метод моментов

Эмпирические моменты

Прежде, чем изложить метод моментов приведем определения эмпирических моментов.

Определение: Эмпирическими моментами порядка k называют среднее значение :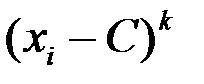

,

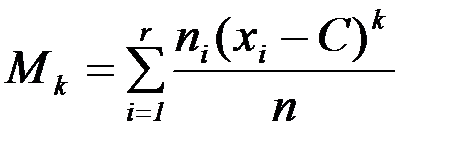где 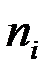– частота варианты,

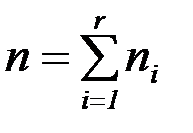– объем выборки,

С – произвольное постоянное число.

Определение: Начальным эмпирическим моментом порядкаk называется эмпирический момент порядка k при С=0:

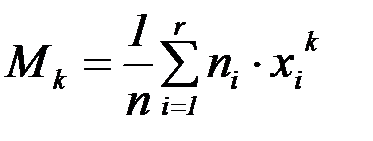
Начальный эмпирический момент первого порядка равен средней выборочной:

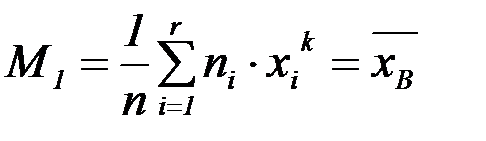
Определение: Центральным эмпирическим моментом порядка k называется эмпирический момент при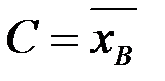

.

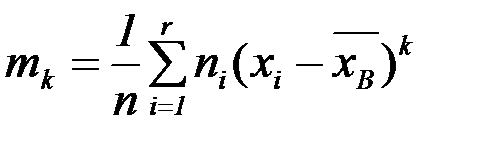Центральный эмпирический момент второго порядка равен выборочной дисперсии:

.

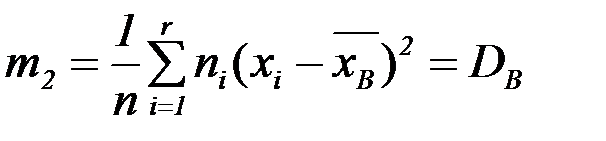Теперь рассмотрим метод моментов для точечной оценки параметров распределения.

Пусть известен вид функции плотности распределения вероятностей случайной величины Χ, зависящей от одного неизвестного параметра ⍬.

Например, для показательного распределения .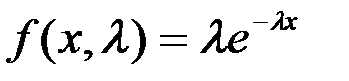

Требуется найти точечную оценку параметра ⍬. В случае показательного распределения ⍬ = λ.

Для получения оценки одного параметра можно использовать одно уравнение с одним неизвестным. В методе моментов в качестве такого уравнения предлагается равенство 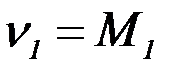, где 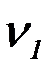– начальный теоретический момент первого порядка; 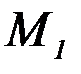– начальный эмпирический момент первого порядка.

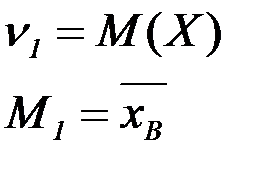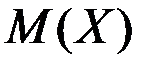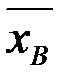=> = (1)

Математическое ожидание можно рассматривать как функцию параметра ⍬:

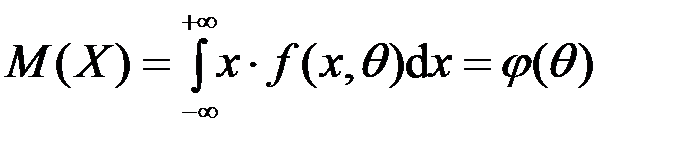(2)

Из формулы (1) можно получить не сам параметр ⍬, а только его оценку, т.к. 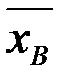является реализацией случайной величины 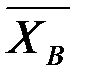. Тогда:

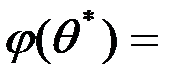
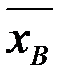(3)

Решив уравнение (3), найдем оценку 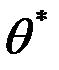, которая является функцией от выборочной средней.

Например, для экспоненциального распределения имеем:

=> , .

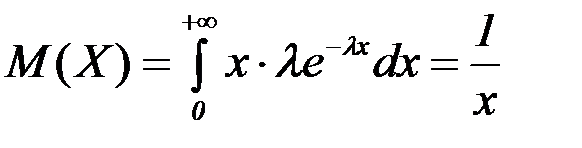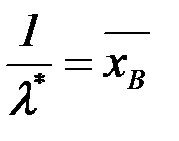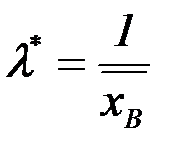Если плотность распределения вероятностей зависит от двух параметров, то ⍬ следует рассматривать как двумерный вектор. Для оценки этих параметров требуется составить не одно, а два уравнения. Такими уравнениями могут быть равенства 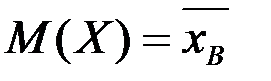, 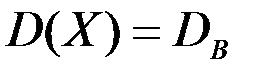или, что более точно, .

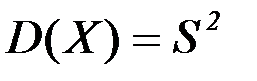Оценка максимального правдоподобия не всегда совпадает с оценкой, найденной методом моментов.

Приведем еще два определения, связанные с понятием момента.

Определение: Асимметрией 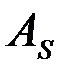эмпирического распределения называется отношение центрального эмпирического момента 3-го порядка к кубу среднего квадратического отклонения. Она характеризует асимметричность распределения случайной величины:

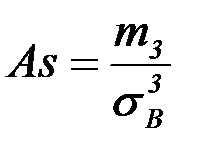
Определение: Эксцессом 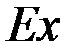эмпирического распределения называется величина, которая определяет частоту появления значений, удаленных от среднего значения:

.

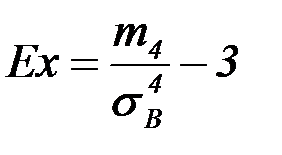Дата добавления: 2014-12-27