Сравнение двух дисперсий нормальных генеральных совокупностей

На практике часто требуется сравнить точность измерения различными приборами и методами.

Пусть имеются две нормально распределенные совокупности X и Y. (Если одну и ту же нормально распределенную случайную величину измеряют двумя приборами, то генеральные совокупности измеряемых значений будут разными – X и Y.)

Из этих генеральных совокупностей извлекают выборки объемом n₁ и n₂ и находят «исправленные» выборочные дисперси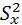и и .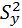

Зададим уровень значимости критерия α.

По данным значениям 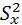, 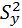и α проверим нулевую гипотезу, состоящую в том, что генеральные дисперсии равны.

Итак, 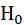: 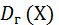= 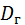(Y).

«Исправленные» дисперсии являются несмещёнными оценками генеральных дисперсий, т. е.

М (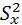) = 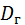(X), M (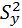) = 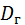(Y),

Поэтому можно представить нулевую гипотезу таким образо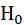м:

: М (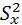) = M ()

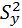Проверим равенство математических ожиданий «исправленных» выборочных дисперсий. В качестве критерия проверки нулевой гипотезы примем отношение большей «исправленной» дисперсии 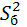к меньшей , т. е. случайную величину: F =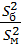

Величина F имеет распределение Фишера-Снедекора со степенями свободы k_{1 =} n₁ - 1, k₂ = n₂ - 1, где n₁ – объем выборки для большей «исправленной» дисперсии, n₂ – для меньшей.

Предположим, что большая дисперсия относится к измерениям X, а меньшая – к измерениям Y.

Тогда в качестве альтернативной гипотезы можно принять

: D (X) > D (Y).

В этом случае критическую область находят из условия:

P (F > F_кр (α, k₁, k₂)) = α (правосторонняя область).

Критическую точку находят по таблице распределения Фишера-Снедекора.

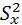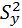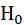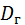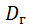Пример: По двум независимым выборкам объемом n₁ = 10 и n₂ = 15 найдены «исправленные» выборочные дисперсии = =12,5, = 7,3. По уровню значимости α = 0,05 проверить нулевую гипотезу : (X)= (Y).

Решение: Находим F_набл:

F_набл = 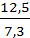= 1,71.

По таблице Фишера-Снедекора при α = 0,05, k₁ = 10 – 1 = 9, k₂ = 15 – 1 = 14 находим F_кр = 2,65.

Т.к. F_набл < F_кр, то нет оснований отвергать нулевую гипотезу.

Заметим, что в тех случаях, когда альтернативная гипотеза может быть представлена в виде 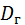(X) ≠ 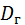(Y), нужно строить двустороннюю область, и уровень значимости можно увеличить. При этом можно ограничиться нахождением правосторонней области для уровня значимости .

Пример: По двум независимым выборкам, объемы которых n₁ = 10 и n₂ = 18, извлеченным из нормальных совокупностей X и Y, найдены «исправленные» выборочные дисперсии 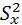= 1,23 и . При уровне значимости α = 0,1 проверить нулевую гипотезу о равенстве генеральных дисперсий при альтернативной гипотезе :

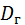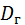(X) ≠ (Y)

Решение: Найдем наблюдаемое значение критерия Фишера-Снедекора:

F_набл = 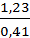= 3.

Здесь критическая область двусторонняя, поэтому уровень значимости принимаем = 0,05, число степеней свободы k₁ = 9, k₂ = 17. По таблице распределения Фишера-Снедекора находим критическую точку F_кр (0,05, 9, 17) = 2,5.

Т.к. F_набл > F_кр, нулевую гипотезу отвергаем.

Если при этом рассматривать два метода или прибора измерения, то предпочтительнее тот, у которого выборочная дисперсия меньше (в нашем примере – 0,41), т. е. совокупность Y.

Дата добавления: 2014-12-27