Например, рассмотрим непараметрический критерий сдвига

Критерий однородности.

Гипотезы о числовых значениях параметров.

Критерии согласия и однородности, проверка

Определение: Критерий однородности – это критерий проверки гипотез о том, что две (или более) выборки взяты из одного распределения вероятностей.

Рассмотрим такую классификацию критериев:

· Параметрические критерии однородности;

· Непараметрические (свободные от распределения) критерии однородности.

Непараметрические (свободные от распределения) критерии однородности не предполагают присутствие какой-либо фундаментальной информации о законе распределения. Любое распределение можно описать параметром положения, характеризующим центр группирования случайных величин, и параметром масштаба, характеризующим степень рассеяния случайных величин относительно центра группирования. Когда закон распределения неизвестен, гипотезы о параметрах проверяются при помощи специальных критериев сдвига и масштаба. Также существуют двухвыборочные критерии согласия.

Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу. Пусть заданы две выборки:

, ,

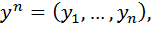
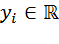взятые из неизвестных непрерывных распределений F(x) и G(y) соответственно.

Нулевая гипотеза 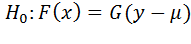. Наиболее частая альтернативная гипотеза .

Если же принимаются какие-либо дополнительные предположения о законе распределения вероятностей, то можно применять параметрические критерии однородности.

К параметрическим критериям однородности относится cравнение параметров нормальных распределений.

Пример: Пусть имеются две выборки независимых случайных величин 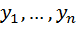. Необходимо, на основе выборочных данных, установить наличие значимой разницы в средних двух совокупностей, из которых извлечены выборки.

Нулевая гипотеза: .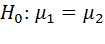

Альтернативы: , , .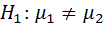

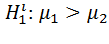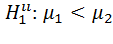Сравнение при известных дисперсиях осуществляется при помощи критерия Стьюдента.

Сравнение при неизвестных равных дисперсиях осуществляется при помощи критерия Стьюдента.

Сравнение при неизвестных неравных дисперсиях осуществляется при помощи модификаций критерия Стьюдента: критерия Кохрена-Кокса, Критерия Сатервайта, критерия Уэлча.

Сравнение двух выборочных средних в связанных выборках осуществляется при помощи критерия Стьюдента.

Критерий Уолша позволяет проверять гипотезу о принадлежности одного наблюдения нормальному распределению, генерирующему выборку.

Существует также двухступентчатый двухвыборочный медианный критерий Волфа.

Критерий Фишера для сравнения двух средних с одинаковыми дисперсиями эквивалентен критерию Стьюдента и основан на связи между распределениями Стьюдента и Фишера.

Историческая справка: Критерий Стьюдента был разработан Уильямом Госсеттом для оценки качества пива на пивоваренных заводах Гиннесса в Дублине (Ирландия). В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсетта вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).

Дата добавления: 2014-12-27