Критерий согласия

Если закон распределения неизвестен, то проверяют нулевую гипотезу: генеральная совокупность распределения по закону А. Проверка производится с помощью специально подобранной величины – критерия согласия.

Определение: Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия: 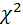(«хи-квадрат») Пирсона, Колмогорова, Смирнова и др.

Проверим гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона.

Будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты. Обычно они различаются.

Критерий не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Пусть по выборке объема n получено статистическое (эмпирическое) распределение:

	…
	…

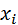
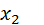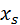
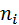
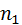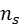
Пусть также вычислены теоретические частоты в предположении нормального распределения.

При уровне значимости α требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально. В качестве критерия проверки нулевой гипотезы примем случайную величину:

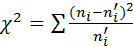(1)

Чем меньше различие частот 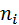и , тем меньше величина .

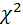Правило: Для того, чтобы при заданном уровне значимости проверить гипотезу 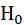«генеральная совокупность распределена нормально», надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия

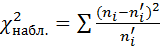(2)

По таблице критических точек распределения 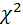по заданному уровню значимости α и числу степеней свободы k=s - 3 (где s – число частичных интервалов) найти критическую точку:

(α;k).

Если 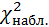< , то нет оснований отвергнуть нулевую гипотезу.

Если 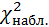> , то нулевую гипотезу отвергают.

Объем выборки должен быть достаточно велик – не менее 50. Каждая группа (интервал) должна содержать не менее 5-8 вариант. Малочисленные группы следует объединять в одну, суммируя частоты.

Для контроля вычислений формулу (2) преобразуют к виду

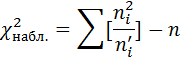
Пример: При уровне значимости 0,1 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирическая и теоретическая частоты:

Эмпирические частоты: 6 13 38 74 106 85 30 14

Теоретические частоты: 3 14 42 82 99 76 37 13

Решение: Вычислим 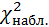, для чего следует составить расчетную таблицу. Получим 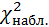=7,19. Контроль вычислений:

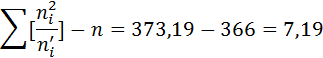
Вычисления произведены правильно. Найдем число степеней свободы, учитывая, что число групп выборки (число частичных интервалов) S = 8; k = 8 - 3 = 5.

По таблице критических точек распределения по уровню значимости α=0,1 и числу степеней свободы k = 5 находим:

(0,1;5) = 9,24.

Т.к. 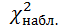< – нет оснований отвергнуть нулевую гипотезу.

Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Большая часть работы заключается в вычислении теоретических частот нормального распределения. Методику вычисления этих частот можно изложить в виде следующего алгоритма.

11.3.Методика вычисления теоретических частот нормального распределения:

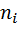· Весь интервал наблюдаемых значений Х (выборки объема n) делят на S частичных интервалов () одинаковой длины. Находят середины частичных интервалов по формуле . В качестве частоты варианты 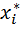принимают число вариант, которые попали в i -й интервал.

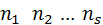
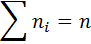
· Вычисляют выборочную среднюю и выборочное среднее квадратическое отклонение .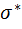

· Нормируют случайную величину Х, т.е. переходят к величине 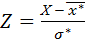и вычисляют концы интервалов :

, ,

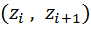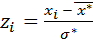причем полагают равным 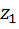= - 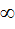(наименьшее значение ),

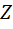а 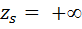(наибольшее значение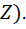

· Вычисляют теоретические вероятности попадания Z в интервалы ( по равенству = 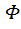( 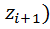- 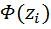, где 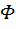(z) – функция Лапласа.

· Находят искомые теоретические частоты .

Дата добавления: 2014-12-27