Многогранники

Тема 6. Многогранники и тела вращения. Образование. Точка и прямая на поверхности. Пересечение поверхности с прямой и плоскостью. Развертка поверхности. Пересечение геометрических тел.

Геометрическая поверхность образуется как совокупность всех последовательных положений линии, движущейся определенным образом в пространстве.

Линия, которая при своем движении образует поверхность, называется образующей.

Образующая может быть прямой линией, в этом случае поверхность называется линейчатой.

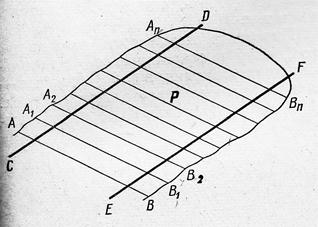
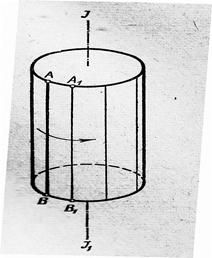
Рис. 43. Рис. 44.

Примером линейчатой поверхности является плоскость P (рис. 43). Она образована движением прямой линии АВ, скользящей по двум параллельным прямым CD и EF. Линейчатой поверхностью будет и цилиндр (рис. 44), образованный вращением прямой линии АВ вокруг оси JJ1, параллельной образующей.

Поверхности, у которых образующие не могут прямыми линиями, называются нелинейчатыми. К таким поверхностям относится, например, сфера. Образующая поверхности может быть неизменяемой, а может в процессе движения деформироваться.

Ограничимся изучением поверхностей с неизменяемой образующей.

Поверхность, полученная вращением образующей вокруг оси, называется поверхностью вращения. Примерами геометрических поверхностей вращения являются поверхности кругового цилиндра, конуса, шара, кольца и т. п.

Поверхность, образованная перемещением (скольжением) образующей по некоторой линии (направляющим), называется поверхностью скольжения. Примерами таких поверхностей являются: плоскость, косая плоскость (гиперболический параболоид), цилиндроид, коноид и т. п.

Часть пространства, ограниченная геометрическими поверхностями, называется геометрическим телом.

Все геометрические тела можно подразделить на две группы: многогранники и криволинейные тела. Рассмотрим подробнее свойства и проекции некоторых геометрических тел.

Геометрическое тело, ограниченное со всех сторон плоскостями, называется многогранником.

Плоские фигуры, ограничивающие многогранник, называются гранями. Грани пересекаются между собой по прямым линиям, которые называются ребрами многогранника. Ребра пересекаются в точках – вершинах многогранника. В каждой вершине сходятся не менее трех ребер.

Многогранники различают в зависимости от формы и количества граней. В технике чаще всего встречаются следующие многогранники:

Призма – многогранник, у которого боковые грани – прямоугольники или параллелограммы, а основаниями служат два равных многоугольника. Призма может быть прямой, если боковые ребра перпендикулярны к основанию, и наклонной, если ребра не перпендикулярны к основанию. Прямая призма называется правильной, если в основании у нее правильный многоугольник. В зависимости от количества сторон основания призмы бывают треугольные, четырехугольные и т. д.

Призма с основаниями в виде параллелограммов называется параллелепипедом. Параллелепипед также может быть прямой и наклонный. Прямой параллелепипед, у которого снованиями являются прямоугольники, называется прямоугольным.

Пирамида – многогранник, у которого боковые грани представляют собой треугольники, имеющие общую вершину. В основании у пирамиды – многоугольник. В зависимости от количества сторон основания пирамида называется трех-, четырех-, пятиугольной и т. д. Пирамида называется правильной, если в основании ее – правильный многоугольник, а боковые грани – равнобедренные треугольники. У правильной пирамиды высота проходит через центр основания. В противном случае пирамида будет неправильной.

Построение проекций многогранника начинают с изображения всех его вершин. Соединив соответствующим образом одноименные проекции вершин, получают проекции ребер и граней многогранника. При этом принято считать, что грани многогранника непрозрачные и поэтому отдельные ребра невидимы и обводятся штриховой линией. При решении вопроса видимости используется способ конкурирующих точек.

Построение проекций призмы и пирамиды рекомендуется начинать строить с проекций основания.

Поверхности рассмотренных многогранников можно рассмотреть в таблице 6.

Таблица 6.

Наименование	Наглядное изображение	Эпюр	Характерные признаки
Прямая призма		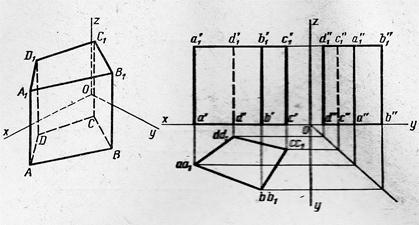Боковые грани – прямоугольники; ребра перпендикулярны к основанию
Наклонная призма		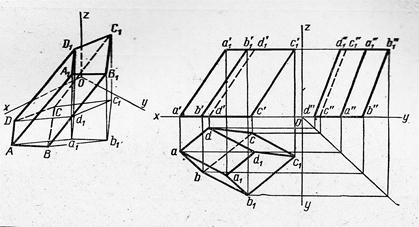Боковые грани – параллелограммы
Правильная призма		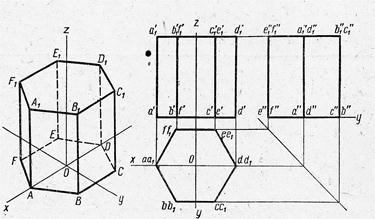Основания - правильные многоугольники; боковые ребра перпендикулярны к основаниям
Параллелепипед		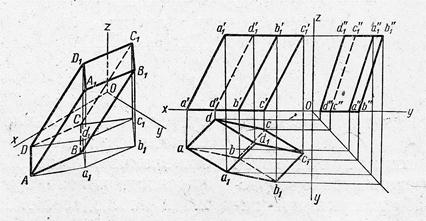Основания - параллелограммы
Прямоугольный параллелепипед		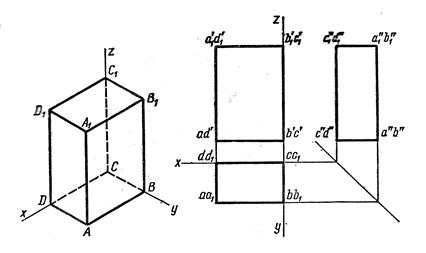Основания- прямоугольники; боковые ребра перпендикулярны к основаниям
Правильная пирамида		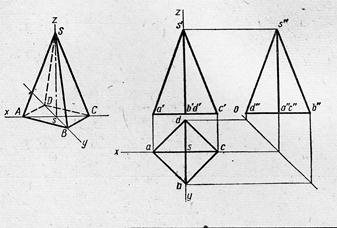Основание- правильный многоугольник; боковые грани -равнобедренные треугольники
Неправильная пирамида		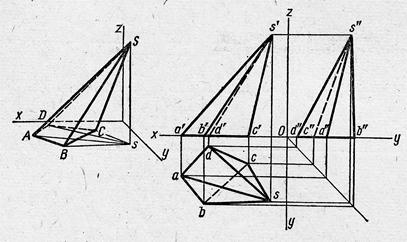Основание- неправильный многоугольник; высота не проходит через центр основания

Дата добавления: 2014-12-27