Пересечение призмы

Сечение геометрических тел проецирующей плоскостью

Для построения линии пересечения поверхности тела плоскостью необходимо найти ряд точек этой линии, т. е. точек, общих для поверхности и плоскости. Соединив последовательно найденные точки на чертеже, определяем линию пересечения. При построении линии пересечения плоскостью линейчатой поверхности (многогранника, конуса или цилиндра) достаточно найти точки пересечения ряда прямых (ребер или образующих), взятых на поверхности, с этой плоскостью, т. е. решить задачу на пересечение прямой с плоскостью.

Форма фигуры сечения призмы плоскостью зависит от взаимного расположения секущей плоскости и призмы. На рисунке представлена прямая треугольная призма в ортогональной проекции; плоскость α, параллельная основанию; плоскость β, наклонная к основанию; плоскость γ, параллельная боковым ребрам (α и β – фронтально-проецирующие плоскости, γ – горизонтально-проецирующая). При пересечении плоскостью α образуется многоугольник, конгруэнтный основанию призмы (рис. 55, б); при пересечении плоскостью β – многоугольник, неконгруэнтный основанию (рис. 55, в); при пересечении плоскостью γ прямоугольник (рис. 55, г).

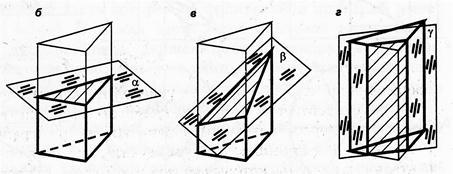
Рис. 55.

В качестве примера на рисунке 56 показано построение проекций линии пересечения поверхности правильной пятиугольной призмы фронтально-проецирующей плоскостью Р. Фигура сечения представляет собой плоский пятиугольник 12345.

Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Р с ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы с фронтальным следом P_V секущей плоскости Р (точки 1ʹ -5ʹ).

Горизонтальные проекции точек пересечения 1 -5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линии связи находят профильные проекции 1ʺ -5ʺ. Полученные точки 1ʺ -5ʺ соединяют прямыми линиями и получают профильную проекцию фигуры сечения.

Действительный вид фигуры сечения можно определить любым из способов: вращения, совмещения или перемены плоскостей проекций.

В данном примере применен способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой Н₁, причем ось x₁ (для упрощения построений) совпадает с фронтальным следом плоскости Р.

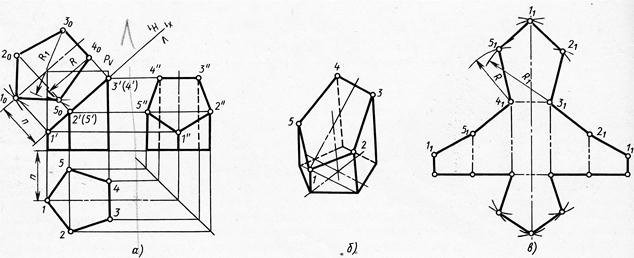
Рис. 56.

Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки 1ʹ восстанавливают перпендикуляр к новой оси x₁ и откладывают на нем расстояние от прежней оси x до прежней горизонтальной проекции точки 1, т.е. отрезок п. В результате получают точку 1₀. Так же находят и новые горизонтальные проекции точек 2 -5. Соединив прямыми линиями новые горизонтальные проекции 1₀ – 5₀, получают действительный вид фигуры сечения.

Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.

К развертке боковой поверхности пристраивают фигуру нижнего основания – пятиугольник и фигуру сечения. Линии сгиба по ГОСТ 2.303-68 показывают на развертке штрихпунктирной с двумя точками.

Для наглядности выполняют построение усеченного тела в аксонометрической проекции. Порядок построения изометрической проекции следующий. Строят изометрическую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на которыхтот основания откладывают их действительные длины, взятые с фронтальной или профильной проекции призмы. Полученные точки 1ʹ -5ʹ соединяют прямыми линиями.

Дата добавления: 2014-12-27