
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для неравнобокого уголка 2 страница
|
|
|
|
3.2 Вопросы для самопроверки
1. Какой вид деформации называется чистым сдвигом?
2. Как записывается закон Гука при сдвиге?
3. Что такое абсолютный сдвиг, относительный?
4. Запишите зависимость между тремя упругими постоянными.
5. Какой вид деформации называется кручением?
6. Какие силовые факторы возникают в поперечном сечении вала при кручении?
7. Какое правило знаков принято для крутящих моментов?
8. Что представляет собой эпюра крутящих моментов и как она строится?
9. Какие допущения положены в основу теории кручения бруса круглого поперечного сечения?
10. Какие напряжения возникают в поперечном сечении круглого бруса и как они направлены?
11. Что такое мембранная аналогия?
12. Какое напряженное состояние возникает в каждой точке круглого бруса при кручении?
13. Что называется жесткостью сечения при кручении?
14. Запишите условие прочности и жесткости при кручении. Какие типы задач решаются по условию прочности и жесткости?
15. Что называется полным и относительным углом закручивания бруса?
4 ИЗГИБ ПРЯМЫХ БРУСЬЕВ
4.1 Общие замечания
Эта тема является самой большой и самой сложной темой курса сопротивления материалов, ее следует изучать постепенно, обратив особое внимание на решение задач. Сначала надо усвоить весьма важные понятия изгибающего момента  и поперечной силы
и поперечной силы  и научиться свободно, строить эпюры
и научиться свободно, строить эпюры  и
и  .
.
В поперечных сечениях балки возникают два внутренних силовых фактора: изгибающий момент  и поперечная сила
и поперечная сила  .
.
В частном случае поперечная сила может быть равна нулю, такой изгиб называется чистым.
Поперечная или перерезывающая сила  , а также изгибающий момент
, а также изгибающий момент  в любом поперечном сечении численно равна алгебраической сумме всех внешних сил, действующих по одну сторону от проведенного сечения. Правило знаков для поперечной силы
в любом поперечном сечении численно равна алгебраической сумме всех внешних сил, действующих по одну сторону от проведенного сечения. Правило знаков для поперечной силы  и изгибающего момента
и изгибающего момента  показаны на рис. (4.1).
показаны на рис. (4.1).
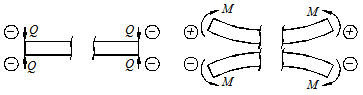
Рисунок 4.1
Поперечная сила  считается положительной, если она поворачивает балку относительно отсеченной части по ходу часовой стрелки.
считается положительной, если она поворачивает балку относительно отсеченной части по ходу часовой стрелки.
Изгибающий момент в сечении считается положительным, если отсеченная часть балки изгибается выпуклостью вниз, т.е. сжатые волокна находятся вверху и наоборот (рис. 4.1).
4.2 Аналитические зависимости
Между изгибающим моментом  , поперечной силой
, поперечной силой  и интенсивностью нагрузки
и интенсивностью нагрузки 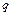 , приложенной к балке, существуют следующие дифференциальные зависимости.
, приложенной к балке, существуют следующие дифференциальные зависимости.
Производная от поперечной силы по координате 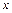 равна интенсивности распределенной нагрузки:
равна интенсивности распределенной нагрузки:
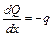
Производная от изгибающего момента по длине стержня равна поперечной силе:
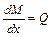 .
.
Вторая производная от изгибающего момента по координате 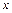 равна интенсивности распределенной нагрузки с обратным знаком
равна интенсивности распределенной нагрузки с обратным знаком
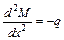
Дифференциальные зависимости между интенсивностью нагрузки 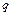 , поперечной силой
, поперечной силой  и изгибающим моментом
и изгибающим моментом  предложены Журавским и носят его имя. С их помощью можно проверять правильность построения эпюр.
предложены Журавским и носят его имя. С их помощью можно проверять правильность построения эпюр.
1. Если на участке балки интенсивность нагрузки 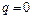 , то на этом участке поперечная сила постоянна, а эпюра изгибающих моментов имеет вид прямой.
, то на этом участке поперечная сила постоянна, а эпюра изгибающих моментов имеет вид прямой.
2. Если на участке балки интенсивность нагрузки 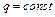 , то на этом участке эпюра поперечных сил имеет вид прямой, а эпюра изгибающих моментов имеет вид квадратной параболы.
, то на этом участке эпюра поперечных сил имеет вид прямой, а эпюра изгибающих моментов имеет вид квадратной параболы.
3. Если на некотором участке балки 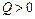 , то эпюра изгибающих моментов возрастает, если
, то эпюра изгибающих моментов возрастает, если 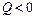 , то эпюра изгибающих моментов убывает.
, то эпюра изгибающих моментов убывает.
4. Если эпюра поперечных сил в некоторой точке 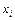 меняет знак с плюса на минус, то в этой точке эпюра изгибающих моментов принимает максимальное значение. Если
меняет знак с плюса на минус, то в этой точке эпюра изгибающих моментов принимает максимальное значение. Если  меняет знак с минуса на плюс, то в этой точке эпюра изгибающих моментов принимает минимальное значение.
меняет знак с минуса на плюс, то в этой точке эпюра изгибающих моментов принимает минимальное значение.
Приведем дополнительно некоторые сведения для проверки правильности построения эпюр.
1. Если балка заканчивается или начинается шарнирной опорой, на которой не приложена нагрузка в виде сосредоточенного момента, то изгибающий момент на этой опоре равен нулю, а поперечная сила по величине равна опорной реакции. Если на опоре приложена нагрузка в виде сосредоточенного момента, то изгибающий момент равен этой нагрузке.
2. Если торец балки не опирается, то поперечная сила на свободном торце балки равна нулю при отсутствии на этом торце сосредоточенной силы, а в случае сосредоточенной нагрузки поперечная сила равна по величине этой нагрузке.
3. Если торец балки не оперт, то изгибающий момент на свободном торце балки равен нулю при отсутствии на этом торце нагрузки в виде сосредоточенного момента, а в случае нагрузки в виде сосредоточенного момента изгибающий момент равен по величине этой нагрузке.
4. Если к балке в некоторой точке 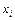 приложена сосредоточенная сила, то эпюра поперечных сил имеет разрыв ("скачок"), равный величине этой силы.
приложена сосредоточенная сила, то эпюра поперечных сил имеет разрыв ("скачок"), равный величине этой силы.
5. Если к балке в некоторой точке 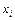 приложен сосредоточенный момент, то эпюра изгибающих моментов в этой точке имеет разрыв ("скачок"), равный величине приложенного момента.
приложен сосредоточенный момент, то эпюра изгибающих моментов в этой точке имеет разрыв ("скачок"), равный величине приложенного момента.
4.3 Прямой чистый изгиб балки
При прямом чистом изгибе балки в поперечных сечениях возникают нормальные напряжения, величина которых зависит от значения изгибающего момента в соответствующем сечении. При прямом поперечном изгибе, кроме того, возникают касательные напряжения, связанные с поперечной силой.
Нормальное напряжение в любой точке по высоте поперечного сечения определяется по формуле Навье:
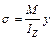 ,
,
где  – изгибающий момент в данном сечении;
– изгибающий момент в данном сечении;
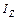 – момент инерции сечения относительно нейтральной оси;
– момент инерции сечения относительно нейтральной оси;
 – расстояние от точки, где определяется напряжение до нейтральной оси;
– расстояние от точки, где определяется напряжение до нейтральной оси;
4.4 Условие прочности при изгибе
Условие прочности при изгибе имеет вид:
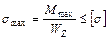 ,
,
где 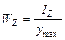 – осевой момент сопротивления.
– осевой момент сопротивления.
Максимальные напряжения растяжения и сжатия для симметричных сечений равны по величине (рис. 4.2).
Напряжения в крайних растянутых и сжатых волокнах для несимметричных относительно нейтральной оси сечений различны (рис. 4.3).
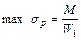 , где
, где 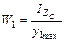 ;
;  где
где 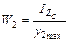
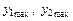 – расстояния от нейтральной оси соответственно для наиболее удаленных точек растянутой и сжатой зон сечения.
– расстояния от нейтральной оси соответственно для наиболее удаленных точек растянутой и сжатой зон сечения.
На рисунках 4.2 и 4.3 знаки напряжений приведены при действии положительного момента. Если момент отрицателен, знаки напряжений меняются на противоположные.
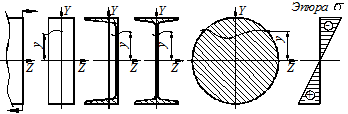
Рисунок 4.2 – Эпюра распределения нормального напряжения
для симметричных сечений
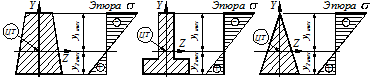
Рисунок 4.3 – Эпюра распределения нормального напряжения
для несимметричных сечений
4.5 Подбор сечения при изгибе
Подбор сечения при изгибе производится по формуле:
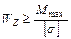 .
.
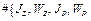 – геометрические характеристики поперечного сечения стержня (балки, вала и т.д.)
– геометрические характеристики поперечного сечения стержня (балки, вала и т.д.)
Для прямоугольного сечения величина 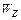 определяется по формуле:
определяется по формуле:
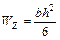 .
.
Для круглого сечения величина 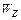 определяется по формуле:
определяется по формуле:
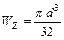 .
.
Для кольцевого сечения величина 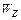 определяется по формуле:
определяется по формуле:
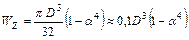 , где
, где 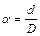 .
.
Диаметр находят из условий прочности
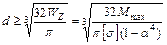 .
.
При подборе прокатных профилей его номер выбирается по сортаменту по найденному 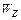 , при этом принимается профиль с ближайшим бóльшим значением
, при этом принимается профиль с ближайшим бóльшим значением 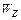 .
.
Задача 4.1
Для заданных двух схем балок (рис. 4.4) требуется написать выражения для поперечных сил  и изгибающего момента
и изгибающего момента  для каждого участка в общем виде, построить эпюры
для каждого участка в общем виде, построить эпюры  и
и  , найти
, найти 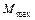 и подобрать:
и подобрать:
а) для схемы, а деревянную балку круглого и прямоугольного поперечного сечения при 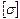 =10 МПа;
=10 МПа;
б) для схемы, б стальную балку двутаврового поперечного сечения при 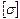 =160 МПа. Для подобранных сечений построить эпюру
=160 МПа. Для подобранных сечений построить эпюру 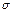 .
.
Пример решения 4.1
Дано: 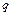 = 6 кН/м;
= 6 кН/м;  =10 кНм;
=10 кНм; 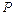 =15 кН;
=15 кН;  = 2;
= 2; 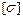 = 10 МПа.
= 10 МПа.
Схема нагружения представлена на рисунке 4.5.
Определить: размеры прямоугольного и круглого поперечного сечения.
Для схемы прямого бруса, построить эпюру внутренних усилий  и
и  .
.
Построить эпюру 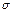 для выбранных сечений.
для выбранных сечений.
Данные взять из таблицы 4.1.
Таблица 4.1
| № п/п | Схема | 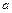 , м , м
| 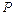 , кН , кН
| 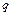 , кН/м , кН/м
|  , кНм , кНм
|
| I | |||||
| II | |||||
| III | |||||
| IV | |||||
| V | |||||
| VI | |||||
| VII | |||||
| VIII | |||||
| IX | |||||
| X | |||||
| е | г | д | е | д |
Решение
1. Разбиваем заданную схему на участки. Составляем выражения для поперечных сил  и изгибающих моментов
и изгибающих моментов  в функции координаты
в функции координаты 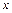 .
.
2. Определяем значения  и
и  на границах участков и в характерных точках.
на границах участков и в характерных точках.
Участок I 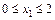
Q1 = qx1
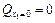 ;
; 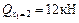 ;
;
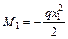 ;
; 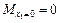 ;
;
 ;
;  .
.
Участок II 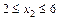
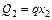 ;
; 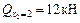 ;
; 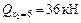
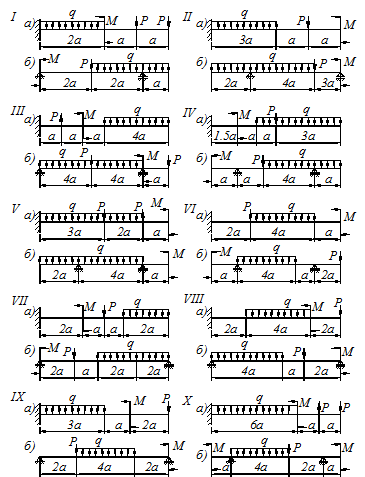
Рисунок 4.4
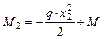 ;
; 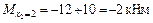 ;
;
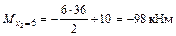 .
.
Участок III 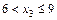 ;
;
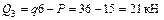 ;
;
 ;
;
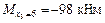 ;
; 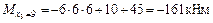 .
.
По полученным данным строим эпюры  и
и  (рис. 4.5)
(рис. 4.5)
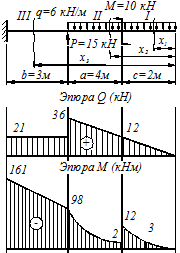
Рисунок 4.5
Величина максимального изгибающего момента равна 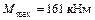 .
.
3. Определим размеры поперечного сечения балки, используя условие прочности при изгибе.
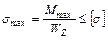
а) прямоугольное сечение 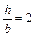 ;
;
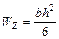 – осевой момент сопротивления для прямоугольного сечения, учитывая заданное соотношение сторон:
– осевой момент сопротивления для прямоугольного сечения, учитывая заданное соотношение сторон: 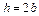 , получим:
, получим:
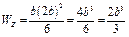 ,
,
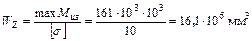 ;
;
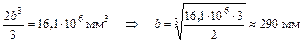 ;
;
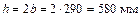 ;
;
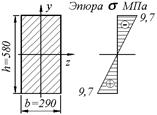
Рисунок 4.6
Максимальное напряжение равно:
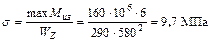 .
.
Недонапряжение составит:
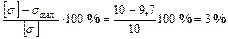 .
.
Прочность бруса обеспечена. Эпюра 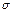 показана на рис. 4.6.
показана на рис. 4.6.
б) круглое сечение
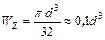 – осевой момент сопротивления для круглого сечения.
– осевой момент сопротивления для круглого сечения.
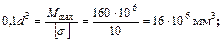
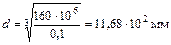
Округляя, принимаем 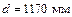 .
.
Максимальное напряжение равно:
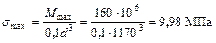
Недонапряжение составит:
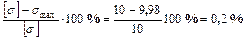
Прочность балки обеспечена. Эпюра s показана на рис. 4.7.
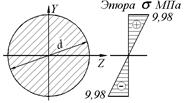
Рисунок 4.7
Пример решения задачи 4.2
Дано: 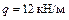 ;
; 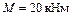 ;
; 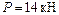 . Расчетная схема представлена на рисунке 4.5.
. Расчетная схема представлена на рисунке 4.5.
Определить: Размеры двутаврового поперечного сечения балки, при 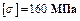 .
.
Построить эпюру 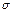 для выбранного сечения.
для выбранного сечения.
1. Определяем реакции опор заданной схемы (рис. 4.8)
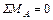 ;
; 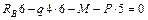 ;
;
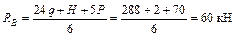 .
.
 ;
; 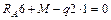 ;
;
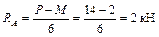 .
.
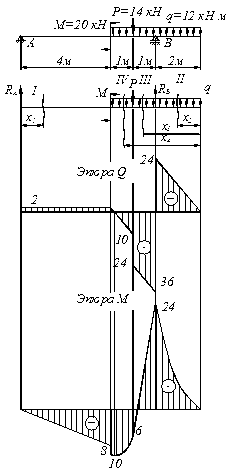
Рисунок 4.8
Проверка
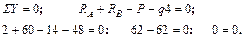
2 Разбиваем заданную схему на участки. Составляем выражения в функции координаты 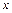 для поперечных сил
для поперечных сил  и изгибающих моментов
и изгибающих моментов  . Определяем значения
. Определяем значения  и
и  на границах участков и в характерных точках.
на границах участков и в характерных точках.
Участок I 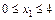
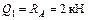 ;
; 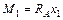 ;
;
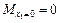 ;
; 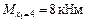
Участок II 
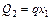 ;
; 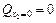 ;
;
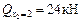 ;
; 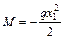 ;
;
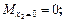
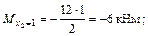
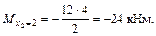
Участок III 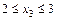
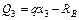 ;
;
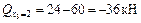 ;
;
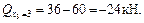
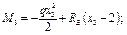
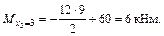
Участок IV 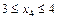
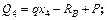
 ;
;

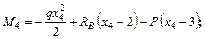
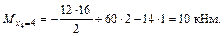
Определим экстремальное значение изгибающего момента, для чего координату 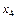 , при которой поперечная сила равна нулю.
, при которой поперечная сила равна нулю.
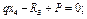
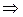
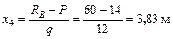 ;
;
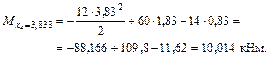
По полученным данным строим эпюры  и
и  (рис. 4.8)
(рис. 4.8)
3. Определим размеры поперечного сечения двутавровой балки по сортаменту, используя условие прочности при изгибе

Максимальный изгибающий момент рамен:
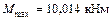
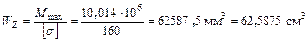
Размеры сечения двутавровой балки определяем из таблицы сортаментов
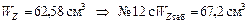
Максимальное напряжение равно:
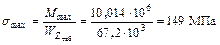 .
.
Недонапряжение составляет:
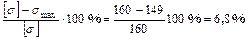
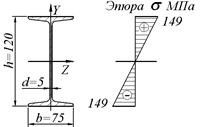
Рисунок 4.9
Прочность балки обеспечена. Эпюра 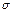 представлена на рисунке. 4.9
представлена на рисунке. 4.9
Задача 4.3
Для показанной на рисунке 4.10 а схемы построить эпюры  и
и  . Определить допускаемую нагрузку
. Определить допускаемую нагрузку 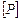 .
.
Дано: 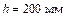 ;
; 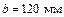 ;
; 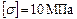 ;
;
Решение
1. Определяем реакции опор.
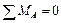 ;
; 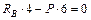 ;
; 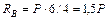 .
.
Проверка
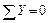 ;
; 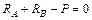 ;
;
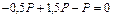 ;
; 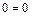 .
.
2. Определяем значения поперечных сил и изгибающих моментов на границах участков
| Участок I | Участок II |
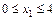
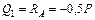 ; ;
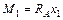 ; ;
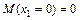 ; ;
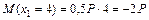 ; ;
| 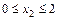
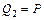 ; ;
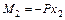 ; ;
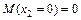 ; ;
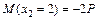 . .
|
3. Эпюры поперечных сил и изгибающих моментов показаны на рисунках 4.10 б и 4.10 в.
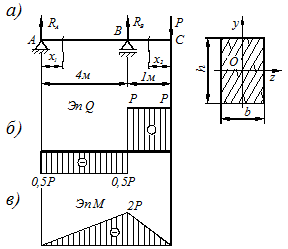
Рисунок 4.10
4. Определим допускаемую нагрузку на балку. Используем условие прочности при изгибе.
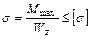
5. Определим осевой момент сопротивления для заданного сечения.
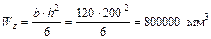
Момент сопротивления из условия прочности равен:
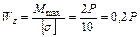 ,
,
тогда приравнивая значения 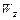 , получим:
, получим:
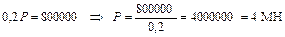
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 718; Нарушение авторских прав?; Мы поможем в написании вашей работы!