Для неравнобокого уголка 4 страница

Например, при одном "лишнем " неизвестном, имеем одно каноническое уравнение:

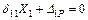
В этих уравнениях перемещения имеют два индекса: первый указывает направление перемещения, второй – причину, вызвавшую это перемещение:

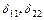– главные перемещения (всегда положительны);

– побочные перемещения;

– грузовые перемещения.

Побочные и грузовые перемещения могут быть положительными, отрицательными и равными нулю.

Задача 5.2

Для плоского статически неопределимого ломаного бруса (рамы), показанного на рисунке 5.4, 5.5 и 5.6 построить эпюры внутренних усилий 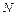, , . Данные взять из табл. 5.2.

Примечание. Студентам заочникам одну из шарнирно-неподвижных опор, заменить шарнирно-подвижной, чтобы задача стала один раз статически неопределимой.

Таблица 5.2

№ вар.	№ стр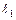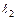.	, м	, м	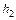, м	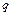, м	, кН/м	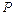, кН	, кНм
1 (III)
2 (I)
3 (II)
4 (I)
5 (II)
6 (III)
7 (I)
8 (II)
9 (III)
0 (I)
г	д	е	е	г	д	е	д	г

Порядок расчета.

1. Установить степень статической неопределимости рамы .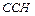

2. Выбрать основную систему (основная система должна быть статически определимой и геометрически неизменяемой).

3. Записать каноническое уравнение метода сил.

4. Построить эпюру изгибающих моментов в основной системе только от заданных внешних нагрузок.

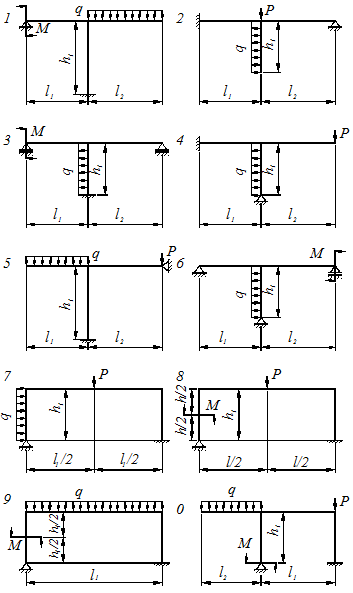
Рисунок 5.4 – Расчетные схемы по I варианту

Рисунок 5.5 – Расчетные схемы по II варианту

Рисунок 5.6 – Расчетные схемы по III варианту

5. Построить в основной системе эпюры изгибающих моментов от единичных сил, приложенных по направлению действия неизвестных усилий.

6. Вычислить коэффициенты канонических уравнений () по формуле интеграла Мора.

7. Вычислить величину неизвестных усилий, ,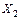

8. Построить эпюры внутренних усилий , , .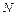

9. Проверить правильность построения эпюр, путем перемножения окончательной эпюры на каждую единичную эпюру , это произведение должно равняться нулю .

.

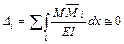Пример решения задачи 5.2.

Дано: ; ; ; .

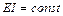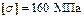Схема рамы представлена на рисунке 5.7.

Рисунок 5.7 – Схема задания

Для заданной рамы раскрыть статическую неопределимость, построить эпюры: нормальной силы, поперечной силы, изгибающего момента и подобрать сечения двутавровой балки.

1. Определяем степень статической неопределимости заданной схемы. Число неизвестных опорных реакций , число возможных уравнений статики для плоской системы сил .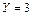

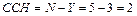
2. Выбираем основную систему, которая должна быть статически определимой и геометрически неизменной. Для этого отбрасываем опорные связи в точке 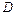рисунок 5.8.

3. Канонические уравнения метода сил имеют вид:

4. Загружаем основную систему только внешней нагрузкой рисунок 5.9 а. Определяем значения изгибающих моментов на границах участков и в характерных точках.

Рисунок 5.8 – Основная система.

Участок I

Участок II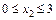

Участок III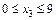

;

;

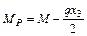
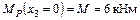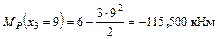
Рисунок 5.9 – Грузовое состояние – а); внутренние силы на третьем участке б).

5. По полученным данным строим эпюру изгибающих моментов рис. 5.10.

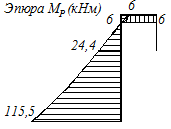
Рисунок 5.10 – Эпюра грузовых изгибающих моментов.

6. Загружаем основную систему единичной силой , определяем значения изгибающих моментов на границах участков рис. 5.11:

Участок I

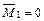
Участок II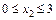

;

;

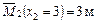
Участок III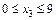

Рисунок 5.11 – Состояние .

Эпюра изгибающих моментов от единичной силы представлена на рисунке 5.12

Рисунок 5.12 – Эпюра единичных изгибающих моментов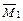

Загружаем основную систему единичной силой 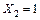рисунок 5.13

Участок I

;

;

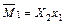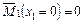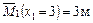
Участок II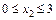

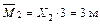
Участок III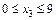

;

;

.

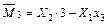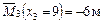Рисунок 5.13 – Состояние .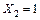

Эпюра изгибающих моментов от единичной силы 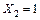представлена на рисунке 5.14

7. Определяем коэффициенты при неизвестных усилиях и свободные члены канонического уравнения по формуле Мора:

,

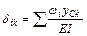
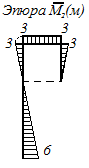
Рисунок 5.14 – Эпюра единичных изгибающих моментов .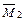

а для вычисления интеграла Мора используем правило Верещагина

а) для определения умножаем эпюру 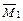саму на себя 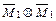по участкам рисунок 5.12;

;

;

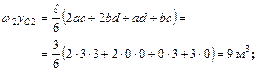
б) для определения умножаем эпюру 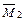саму на себя 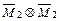рисунок 5.14;

;

;

;

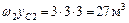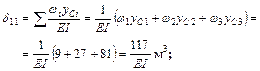
в) для определения и перемножаем эпюры (рис. 5.12 и 5.14). На основании теоремы о взаимности перемещений ;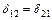

; ;

;

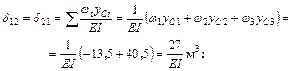
г) для определения 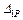перемножаем эпюры 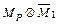(рис. 5.10 и 5.12).

; ;

;

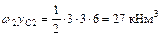д) для определения 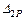перемножаем эпюры 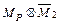(рис. 5.10 и 5.14).

; ;

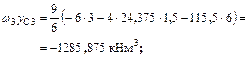
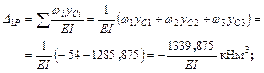
8. Проверяем правильность найденных значений коэффициентов. Для этого вычисляем сумму всех коэффициентов системы.

;

;

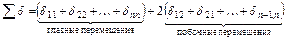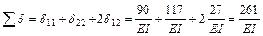Строим суммарную эпюру изгибающий моментов 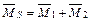от единичных сил рисунок 5.15.

; .

;

; ;

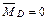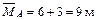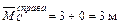Умножаем эпюру саму на себя рисунок. 5.15, получаем величину .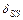

;

;

;

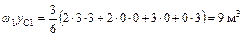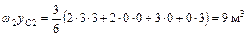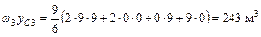Рисунок 5.15 – Суммарная эпюра изгибающих моментов.

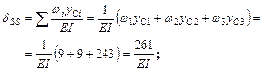
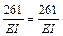; , т.е. единичные коэффициенты найдены, верно.

Сумма свободных членов канонической системы уравнений:

,

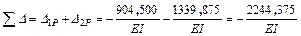должна быть равна величине 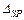, для определения которой, перемножаем эпюры 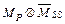(рис. 5.10 и 5.15)

;

;

;

; .

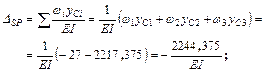
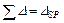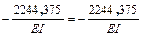Значения свободных членов канонической системы уравнений найдены верно.

9. Полученные значения коэффициентов подставляем в систему канонических уравнений метода сил.

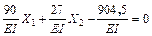
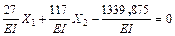
Решая полученную систему уравнений, находим значения сил 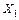и :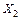

; .

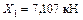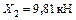Статическая неопределимость системы раскрыта.

10. Загружаем основную систему рисунок 5.8 заданными внешними нагрузками и найденными силами (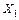, 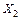) рис. 5.16. Определяем значения внутренних силовых факторов 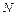, и на границах участков:

Участок I

; ;

;

;

;

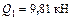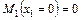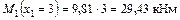Участок II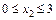

; ;

;

;

;

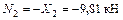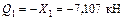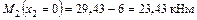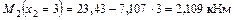Рисунок 5.16

Участок III ; ; ; ; ; ;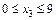

;

;

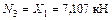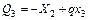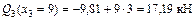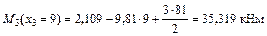По полученным данным строим эпюры 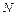, и рисунок 5.17, 5.18, 5.19.

11. Проверяем правильность эпюры изгибающих моментов. Деформационная проверка. Перемножаем эпюры (рис. 5.12, 5.19).

;

;

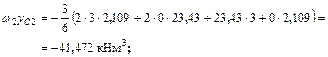
Итак, вертикальные перемещения О.С. равно

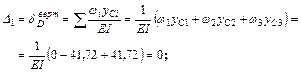
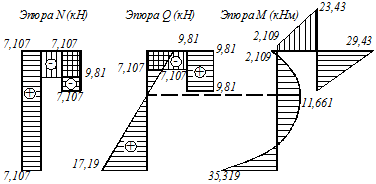
Рисунок 5.17

Рисунок 5.18

Рисунок 5.19

Аналогично получаем , тогда деформационные проверки выполняются.

Пример решения задачи 5.3

Для заданной схемы раскрыть статическую неопределенность, построить эпюры: нормальной силы, поперечной силы, изгибающего момента.

Дано: ; .

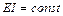Заданная схема балки представлена на рис. 5.20

1. Определяем степень статической неопределимости заданной схемы

2. Выбираем основную систему, которая должна быть статически определимой и геометрически неизменной, рис. 5.21.

Рисунок 5.20

Порядок расчета задачи 5.3

3. Для заданной системы записываем канонические уравнения метода сил.

4. Загружаем основную систему только внешней нагрузкой рис. 5.21. Определяем реакции опор только от заданной внешней нагрузки (рис. 5.22).

; ;

;

; ;

;

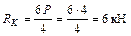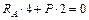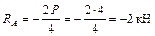Рисунок 5.21

Проверка

; ;

; ;

; .

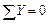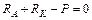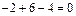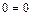Рисунок 5.22

5. Определяем значения изгибающих моментов на границах участков.

Участок I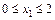

; ;

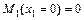Участок II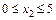

Участок III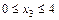

; ;

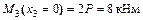По полученным данным строим эпюру изгибающего момента (рис. 5.23).

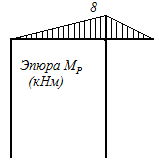
Рисунок 5.23

6. Загружаем основную систему только единичной силой рисунок 5.24.

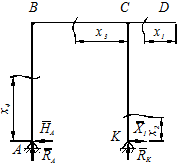
Рисунок 5.24

Определяем реакции опор

; ;

; ;

; ;

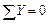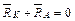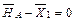Определяем значения изгибающих моментов на границах участков.

;

; ;

;

;

; ;

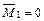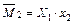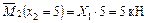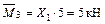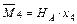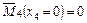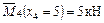
По полученным данным строим эпюру изгибающего момента (рис. 5.25) от единичной силы.

Рисунок 5.25

7. Определяем значение коэффициента при неизвестной силе и свободный член канонического уравнения, используя правило Верещагина:

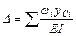
а) для определения умножаем эпюру 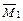саму на себя (рис. 5.25)

;

;

;

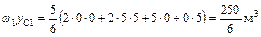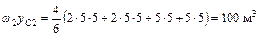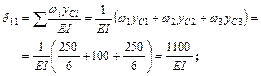
б) для определения 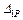перемножаем эпюры 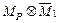(рис 5.23 и 5.25).

; ;

;

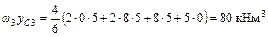Дата добавления: 2014-12-27