Для неравнобокого уголка 6 страница

Уравнений составляется столько, какова степень статической неопределимости.

Полученной уравнение называется уравнением трех моментов, т.к. оно устанавливает связь между тремя последовательными опорными моментами.

Рассмотрим пример составления уравнения трех моментов для балки с жесткой заделкой и консолью рис. 6.2 а.

Основная система изображена на рис. 6.2 б.

Эта балка один раз статически неопределима, т.к. в фиктивном пролете 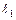нет нагрузки, т.е. защемлена одним концом, то 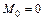, также равна нулю "грузовая" площадь .

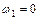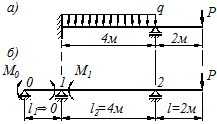
Рисунок 6.2

Для первой промежуточной опоры уравнение трех моментов имеет вид:

.

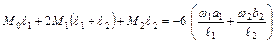Основным неизвестным является момент . Нагрузка на консоли 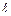влияет на площадь эпюры грузовых моментов 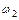и тогда 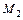считается равным нулю. Проще отнести нагрузку на консоли к опорному моменту, т.е. положить 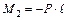, и не учитывать ее влияние на эпюру 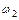, которая зависит только от нагрузки во втором пролете.

После решения системы уравнений трех моментов статическая неопределимость балки будет раскрыта, т.е. найдены все опорные моменты.

Окончательная эпюра изгибающих моментов строится как сумма эпюр от опорных моментов 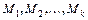и от нагрузки 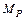. Причем сумма эпюр от опорных моментов имеет вид ломаной со значениями 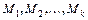на опорах. Эпюру моментов от опорных моментов называют линией опорных моментов (Л.О.М.). К ней подвешивается эпюра 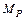и получается окончательная эпюра .

Задача 6.1

Для заданной неразрезной балки (рис. 6.3, 6.4, 6.5) требуется:

1. Построить эпюры и .

2. Найти опорные реакции.

3. Подобрать прочные размеры двутавровой балки, приняв .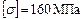

Данные взять из таблицы 6.1.

Примечание. В зависимости от графика учебного процесса и специализации, особенно для студентов-заочников, одну шарнирно-подвижную опору из рисунка 6.3, 6.4, 6.5 можно убрать, чтобы задача стала один раз статически неопределимой.

Таблица 6.1

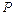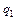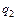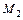№ строки и вар.	Схема №	Длина пролетов, м	, кН	, кН/м	, кН/м	, кНм	, кНм
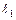
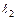
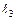
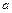
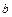
1 (I)
2 (III)
3 (II)
4 (III)
5 (I)
6 (II)
7 (III)
8 (II)
9 (III)
0 (I)
д	е	г	д	е	г	д	е	г	д	е	г

Порядок расчета задачи 6.1

1. Определить степень статической неопределимости заданной системы и выбрать основную систему.

2. Записать уравнения трех моментов в общем виде.

3. Рассматривая каждый пролет как балку, лежащую на двух опорах с внешней нагрузкой, определить реакции опор и построить эпюру изгибающих моментов в основной системе .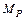

4. Вычислить "грузовые" площади эпюры изгибающих моментов 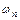на каждом пролете и, соответственно, расстояния от их центров тяжести до левой 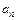и правой 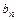опор, .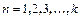

5. Полученные значения (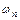, , 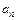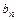и т.д.) подставляют в уравнения трех моментов. Вычисляют опорные моменты, решая систему уравнений трех моментов.

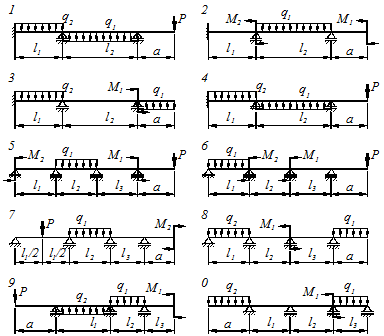
Рисунок 6.3 – Расчетные схемы по I варианту.

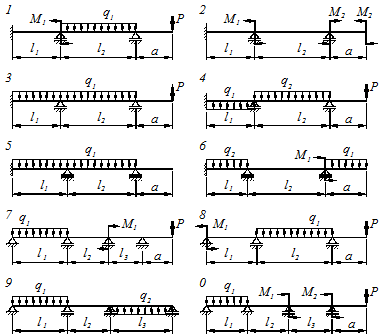
Рисунок 6.4 – Расчетные схемы по II варианту.

6. Рассматривая каждый пролет как балку, лежащую на двух опорах с найденными опорными моментами с учетом их знаков определить реакции опор; выполнить проверку правильности найденных опорных реакций.

7. Произвести общую (статическую) проверку найденных опорных реакций всей балки.

8. Построить эпюры и для заданной неразрезной балки.

9. Определить из условия прочности необходимый размер поперечного сечения двутавровой балки.

Пример решения задачи 6.1

Для представленной на рисунке 6.6 неразрезной балки раскрыть статическую неопределимость, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения двутавровой балки.

Дано: ; ; ; ;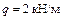

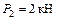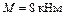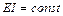
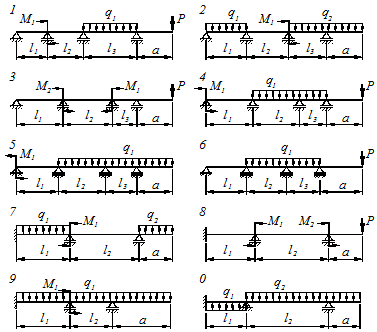
Рисунок 6.5 – Расчетные схемы по III варианту

Порядок расчета задачи 6.1

1. Определяем степень статической неопределимости заданной схемы.

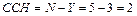
2. Записываем уравнения трех моментов в общем виде.

,

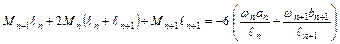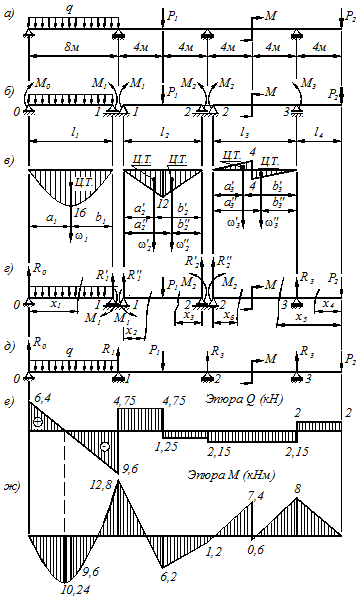
Рисунок 6.6

где индекс означает нумерацию опор, которую выполняют слева направо, начиная с нуля, а пролеты нумеруют, начиная с единицы. Над опорами устанавливаем положительные изгибающие моменты (рис. 6.6 б).

Уравнения трех моментов составляем только для промежуточных опор.

При

;

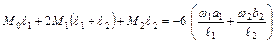При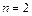

;

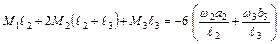3. Рассматривая каждый пролет как балку, лежащую на двух опорах без консольной части, определяем реакции опор и значения изгибающих моментов на границах участков каждого пролета.

Пролет

; ;

;

; ;

;

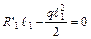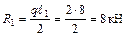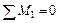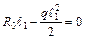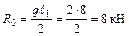Проверка

; ;

; ;

; ; ;

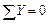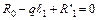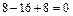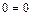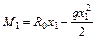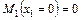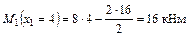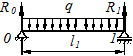Рисунок 6.7

Пролет

; ; ;

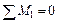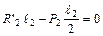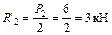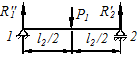Рисунок 6.8

; ;

;

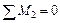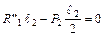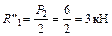Проверка

; ;

; ;

; ;

;

; ;

;

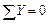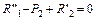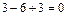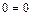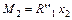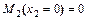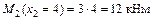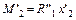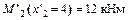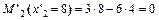Пролет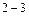

; ; ;

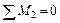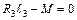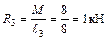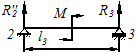Рисунок 6.9

; ;

;

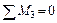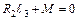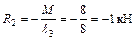Проверка

; ;

; ;

; ;

;

; ;

;

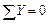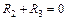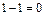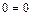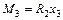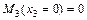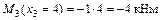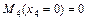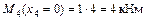4. По полученным данным строим эпюру изгибающего момента для каждого пролета в отдельности (рис. 6.6 в).

5. Определяем значения площадей изгибающего момента каждого пролета и расстояния от их центров тяжести до правой и левой опор.

; ;

; ;

;

;

;

; ;

; ;

;

; ; ; ;

; ; ;

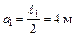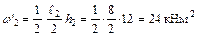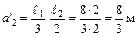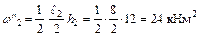
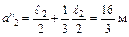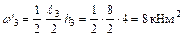
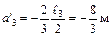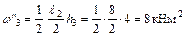
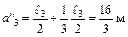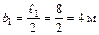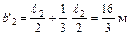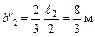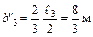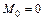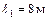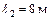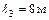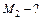Полученные значения площадей и расстояний подставляем в уравнения трех моментов.

;

;

;

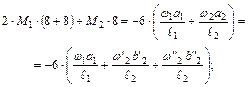
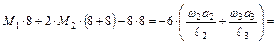
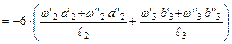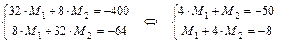6. Решая систему уравнений с двумя неизвестными определим значения опорных моментов и :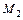

;

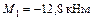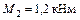
Проверка правильности решения системы уравнений:

;

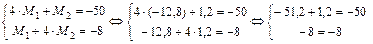7. Рассматривая каждый пролет как балку, лежащую на двух опорах с найденными опорными моментами с учетом их знаков, определяем реакции опор.

Пролет

; ; ; ; ; ;

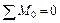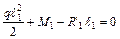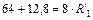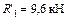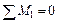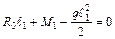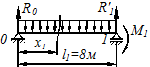Рисунок 6.10

;

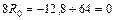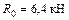
Проверка

; ;

; ;

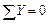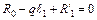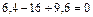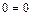Пролет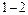

; ; ; ;

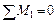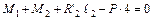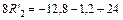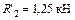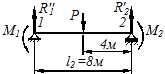Рисунок 6.11

; ; ;

; ;

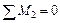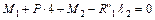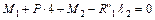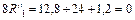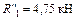Проверка

; ;

; ;

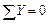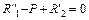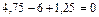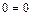Пролет с учетом консоли

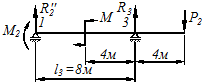
Рисунок 6.12

; ;

; ;

;

; ;

; ;

;

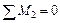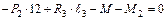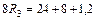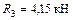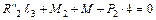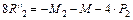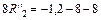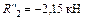Проверка

; ;

; ;

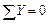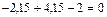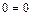8. Определяем полные значения опорных реакций.

;

;

;

;

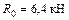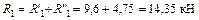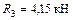Полная проверка равновесия системы:

; ;

; ;

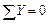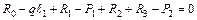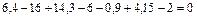9. Загружаем заданную схему внешней нагрузкой и найденными опорными реакциями (рис. 6.6 г). Разбиваем заданную схему на участки. Определяем значения и на границах участков обычным способом.

Участок I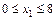

;

;

; ;

;

.

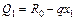
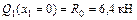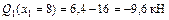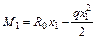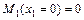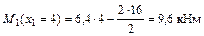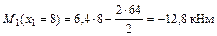Экстремальное значение изгибающего момента

; ; ;

.

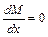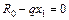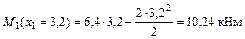Участок II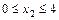

;

; ;

.

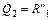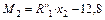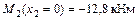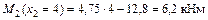Участок III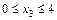

;

;

.

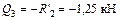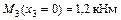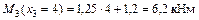Участок IV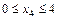

;

; ;

.

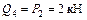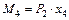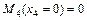Участок V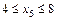

;

; ;

.

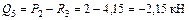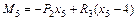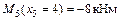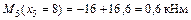Участок VI

;

; ;

.

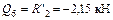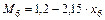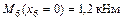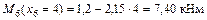По полученным данным строим эпюры поперечных сил и изгибающих моментов (рис. 6.6 е; 6.6 ж).

10. Определяем размеры поперечного сечения двутавровой балки.

; .

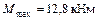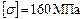Из условия прочности при изгибе имеем:

;

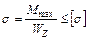
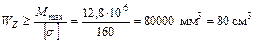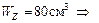двутавровая балка № 14, .

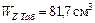Максимальное напряжение равно:

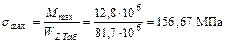
Недонапряжение составляет:

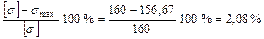
Прочность балки обеспечена

Пример решения задачи 5.3 с использованием уравнения трех моментов

1. Определяем степень статической неопределимости заданной схемы.

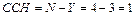
2. Заменяем защемление дополнительным пролетом. Отбрасываем консольную часть балки. Нумеруем опоры слева направо, начиная с нуля, а пролеты, начиная с единицы. Загружаем схему положительными опорными моментами (рис. 6.13 б).

3. Записываем уравнение трех моментов для заданной схемы. Уравнение трех моментов составляем для промежуточных опор.

;

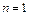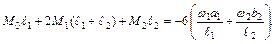
4. Рассматривая каждый пролет как балку, лежащую на двух опорах, (рис. 6.13в) определяем реакции опор. Строим эпюру изгибающих моментов (рис. 6.13 г).

Пролет

; ;

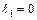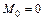Дата добавления: 2014-12-27