Решение. Задача один раз статически неопределимая

Задача один раз статически неопределимая. Примем усилия 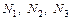в стержнях растягивающими (рис.1.16 б). Составим уравнения равновесия статики:

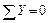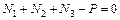; ; (1)

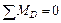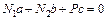; (2)

Для составления дополнительного уравнения, учитывая совместность деформаций всех стержней, рассмотрим систему в деформированном состоянии (рис.1.16 в):

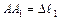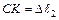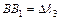; ; ; (3)

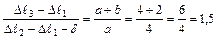– уравнение совместности деформаций.

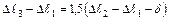
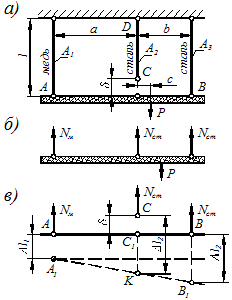
Рисунок 1.16

Значения, входящие в это уравнение деформаций (с учетом влияния температуры) будут следующими:

;

;

;

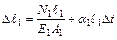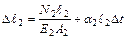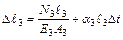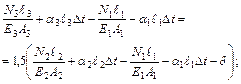
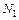– медь;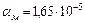

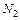– сталь; 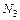– сталь;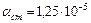

;

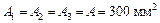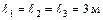
Подставив числовые данные и решая совместно уравнения 1, 2, 3 определим усилия в стержнях .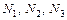

; ; .

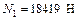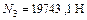Напряжения в стержнях:

;

;

.

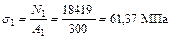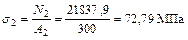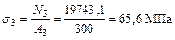1.4 Вопросы для самопроверки

1. Какой вид деформации называется центральным растяжением или сжатием?

2. Как вычисляется значение продольной силы в произвольном поперечном сечении бруса?

3. Что представляет собой эпюра продольных сил и как она строится?

4. Как проверить правильность построения эпюры продольной силы? Дифференциальная зависимость между 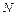и .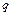

5. Записать закон Гука.

6. Как определить напряжения и деформации при растяжении и сжатии? Условия прочности и жесткости.

7. Как используется гипотеза плоских сечений (гипотеза Бернулли) для выяснения закона распределения нормальных напряжений в поперечном сечении растянутого (сжатого) бруса?

8. Что представляют собой величины 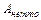и 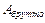поперечного сечения бруса.

9. Что называется модулем продольной упругости 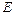? Как влияет величина 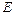на деформации бруса?

10. Как формулируется закон Гука? Напишите формулы абсолютной и относительной продольных деформаций.

11. В каких координатах строится диаграмма растяжения?

12. Что называется пределом пропорциональности, упругости, текучести, прочности? Что представляет собой площадка текучести?

13. Какие деформации называются упругими и, какие остаточными или пластическими?

14. Какое явление называется наклепом?

15. Чем отличается диаграмма сжатия чугуна от диаграммы растяжения?

16. Каково поведение материала при разгрузке и повторном нагружении?

17. Что такое модуль упругости? Для чего он необходим?

18. Что такое коэффициент поперечной деформации? Как он определяется?

19. Какие материалы называются анизотропными?

20. Какие действия нагрузки называются статическими?

21. Какие системы называются статически неопределимыми?

22. Что представляют собой дополнительные уравнения?

23. Что называется степенью статической неопределимости системы?

24. Какие напряжения называются монтажными?

25. Какое напряжение называется температурным?

26. Какие напряжения называются местными?

27. Что называется теоретическим коэффициентом концентрации напряжений?

28. Что представляет собой допускаемая, предельная и предельно допускаемая нагрузка?

29. Как отражается увеличение жесткостей отдельных элементов статически неопределимых систем на усилиях в этих и других элементах?

2 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

В теории изгиба очень важную роль играют моменты инерции. Этот вопрос следует изучить предварительно в виде самостоятельной темы.

2.1 Статические моменты

Статическими моментами относительно осей и 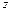называют интегралы вида (рис. 2.1).

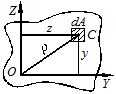Рисунок 2.1

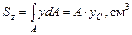
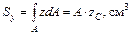
отсюда получаем формулы для определения координат центра тяжести любой сложной фигуры, которые имеют вид:

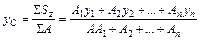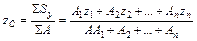, см;

, см,

где 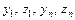– расстояние от центров тяжести каждой фигуры соответственно до осей OZ и OY.

2.2 Осевые моменты инерции

Осевыми (экваториальными) моментами инерции относительно осей и 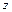называют интегралы вида

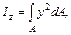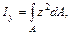см⁴, см⁴.

2.3 Центробежные моменты инерции

Центробежным моментом инерцииотносительно осей и 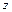называют интеграл вида

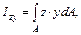см⁴.

2.4 Полярные моменты инерции

Полярным моментом инерцииотносительно точки 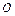(рис. 2.1) называют интеграл вида

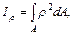
где 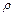– расстояние до полюса, точки 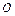(рис.2.1), определяемое выражением:

.

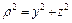Сумма осевых моментов инерции сечения относительно двух координатных осей равна полярному моменту инерции относительно начала координат.

.

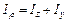Осевые и полярные моменты инерции – величины положительные; центробежный момент инерции может быть положительным, отрицательным и равным нулю.

2.5 Параллельный перенос осей

Параллельный перенос осейсправедлив только в том случае, если ось 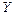проходит через центр тяжести сечения.

Момент инерции сечения относительно произвольной оси равен моменту инерции относительно центральной параллельной оси плюс произведение площади сечения на квадрат расстояния между осями (рис. 2.2)

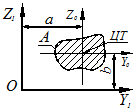
Рисунок 2.2

;		;
;		;
		,

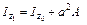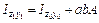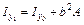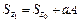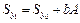где 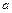и 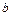– расстояния между параллельными осями или координаты центра тяжести в осях .

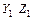2.6 Изменение моментов инерции при повороте координатных осей

Если известны моменты инерции сечения относительно осей 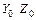, , 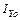, , 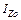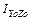то при повороте осей на угол 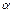против часовой стрелки, моменты инерции относительно повернутых координатных осей: 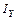, , 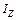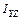определяют по формулам:

;

;

.

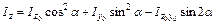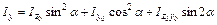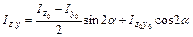2.7 Главные оси и главные моменты инерции

Главными осями инерции называют оси относительно, которых центробежный момент инерции равен нулю.

Осевые моменты инерции относительно главных осей приобретают экстремальные значения ().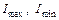

Центробежный момент инерции сечения относительно двух взаимно-перпендикулярных осей, одна из которых является осью симметрии, равен нулю. Следовательно, две взаимно-перпендикулярные оси, одна из которых ось симметрии, являются главными осями инерции.

Оси, проходящие через центр тяжести сечения, называют центральными. Главные оси, проходящие через центр тяжести, называют главными центральными осями.

2.8 Главные моменты инерции

Если известны моменты инерции относительно центральных осей, то для произвольного сечения, главные моменты инерции могут быть найдены по формуле:

.

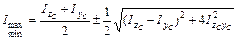2.9 Положение главных центральных осей

Положение главных центральных осей вычисляют по формуле:

,

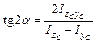если значение угла поворота отрицательно, то центральные (случайные) координатные оси следует повернуть по ходу часовой стрелки.

Для проверки правильности вычисления 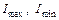можно использовать равенство

.

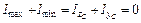2.10 Центробежный момент уголка

При определении центробежного момента уголка (равнобокого или неравнобокого) сначала можно найти центробежный момент инерции всего уголка относительно осей, проходящих через центр тяжести параллельно полкам, при помощи формулы:

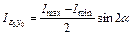
где 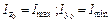– главные центральные моменты инерции, величины которых даны в таблице сортамента.

Дата добавления: 2014-12-27