Решение. 1. Определим усилие в стержне (рис

1. Определим усилие в стержне (рис. 1.6 б), используя уравнение моментов относительно точки 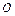, предварительно расставив реакции

;

;

;

;

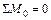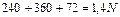Таблица 1.5

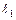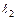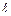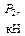
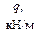
№ вар.	, м	, м	, м	K					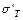, МПа	, МПа
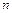
	1,0	1,5		0,5							1,8
	1,2	2,0	1,5	0,4							1,6
	1,4	1,6	1,6	0,3							1,5
	1,5	2,0	1,8	0,6							1,4
	1,6	2,0	1,8	0,7							1,5
	2,0	1,5	1,8	0,4							1,6
	1,5	1,8	2,0	0,5							1,7
	1,6	2,0	1,8	0,3							1,8
	1,8	1,5	1,4	0,6							1,6
	2,0	1,2	2,0	0,4							1,5
	д	е	е	г	д	е	д	г	Е	е	д

2. Определим размеры круглого поперечного сечения стержня BD, используя условие прочности при растяжении и сжатии

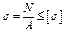
Участок ВС

=4 м

=2 м

kl₁ =1,2 м

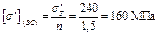
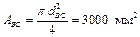
Рисунок 1.8

Принимаем

Участок CD

;

;

;

;

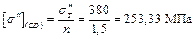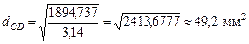Принимаем .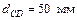

3. Определим удлинение стержня по участкам

;

;

;

;

.

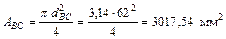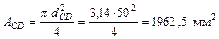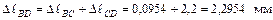4. Определим величину опускания т. 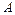. Рассмотрим систему в деформированном состоянии (рис.1.6 б)

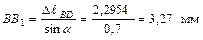
Рассматривая подобие треугольников 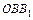и 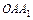определим величину опускания т.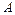

.

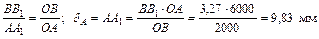Величина опускания т. 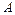равна .

5. Определим вес стержня ВД

1.3 Статически неопределенные задачи при растяжении и сжатии

Статически неопределенными называются конструкции, в элементах которых для определения усилий недостаточно уравнений статики. Кроме уравнений статики при решении статически неопределенных задач необходимо использовать также уравнения, учитывающие деформации элементов конструкций (уравнения совместности деформаций).

Все статически неопределимые конструкции имеют так называемые "лишние", с точки зрения статики, связи в виде закрепления, стержней и других элементов.

При одной "лишней" неизвестной система называется один раз или однажды статически неопределимой, при двух – дважды статически неопределимой и т.д.

Степень статической неопределимости плоской системы может быть определена по формуле:

,

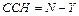где 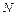– число неизвестных внутренних силовых факторов;

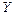– число уравнений статики.

Решение статически неопределимых задач проводят в четыре этапа.

Дата добавления: 2014-12-27