
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрическая сторона задачи
|
|
|
|
Статическая сторона задачи
Составляют уравнения равновесия отсеченных элементов конструкции, содержащие неизвестные усилия.
Рассматривают заданную систему в деформированном состоянии, т.е. изображают план перемещений, по которому устанавливают связь между деформациями отдельных элементов конструкции. Полученные уравнения называют уравнениями совместности деформации. Их всегда возможно составить столько, сколько "лишних" неизвестных.
3. Физическая сторона задачи
В уравнениях совместности выражают деформации элементов конструкции на основании закона Гука через действующие в них неизвестные усилия.
4. Синтез
Решают полученные уравнения равновесия и совместности деформации относительно искомых неизвестных усилий.
Задача 1.4
Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум (трем для стационара) упругим стержням (рис. 1.9).
Определить максимальную величину нагрузки 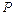 , при которой система работает в упругой стадии, и сравнить с предельной грузоподъемностью системы (несущей способностью системы)
, при которой система работает в упругой стадии, и сравнить с предельной грузоподъемностью системы (несущей способностью системы) 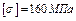 .
.
Значения взять из таблицы 1.6.
Порядок расчета
1. Для абсолютно жесткого бруса записать уравнение равновесия.
2. Из анализа системы в деформированном состоянии нагруженного жесткого бруса, изобразить план перемещений и записать уравнения совместности деформаций стержней.
3. Выразить удлинения стержней через усилия в них и подставить в уравнение деформаций.
4. Решить систему из двух (трех) уравнений, полученных в п. 2 и 3, выразить неизвестные усилия в стержнях через силу 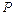 .
.
5. Определить напряжения в стержнях, выразив их через силу 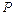 .
.
6. Из условия прочности при растяжении-сжатии  вычислить максимальное значение
вычислить максимальное значение 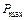 , при котором система работает в упругой стадии.
, при котором система работает в упругой стадии.
7. Вычислить несущую способность каждого стержня в отдельности из условия 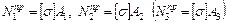 .
.
8. Подставить величину 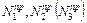 в уравнение равновесия (п. 1) и вычислить предельную грузоподъемность системы
в уравнение равновесия (п. 1) и вычислить предельную грузоподъемность системы 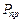 .
.
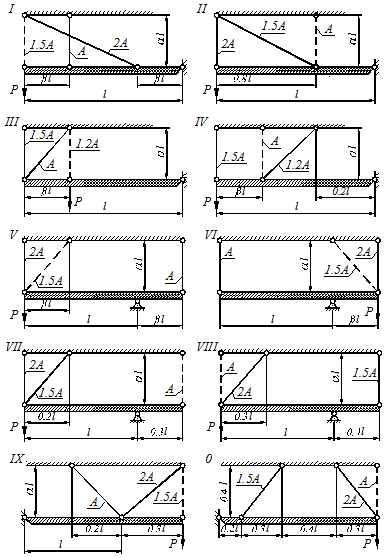
Рисунок 1.9
Таблица 1.6
| № строки | № схемы | 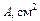
| 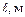
| 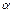
| 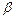
|
| I | 0,45 | 0,4 | |||
| II | 0,5 | 0,4 | |||
| III | 0,4 | 0,5 | |||
| IV | 0,7 | 0,3 | |||
| V | 0,4 | 0,5 | |||
| VI | 0,3 | 0,5 | |||
| VII | 0,6 | 0,4 | |||
| VIII | 0,5 | 0,3 | |||
| IX | 0,6 | 0,4 | |||
| X | 0,4 | 0,5 | |||
| е | д | г | е | д |
9. Сравнить величины 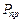 и
и 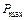 .
.
Примечание: Для студентов стационара следует добавить третий стержень (на рисунке показан пунктиром).
Пример решения задачи 1.4
1. Определить для заданной стержневой системы максимальную величину нагрузки 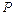 при работе в упругой стадии и предельную грузоподъемность системы (рис. 1.10)
при работе в упругой стадии и предельную грузоподъемность системы (рис. 1.10)
Дано: 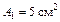 ;
; 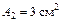 ;
; 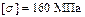 ;
; 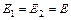 .
.
1. Статическая сторона задачи
1. Определим степень статической неопределимости заданной системы.
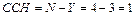
2. Составим уравнения статики. В данном случае уравнение моментов относительно т. 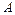 .
.
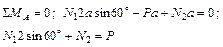 I
I
2. Геометрическая сторона задачи
3. Рассмотрим систему в деформированном состоянии (рис. 1.10 в). Из подобия треугольников следует
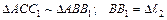 ;
;
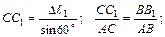
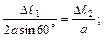
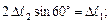 II
II
где II – уравнение совместности деформаций.
3. Физическая сторона задачи
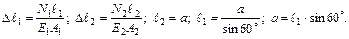
4. Синтез
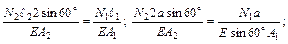
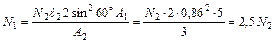
Значение силы 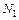 подставим в уравнение I.
подставим в уравнение I.
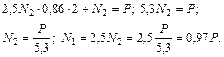
4. Определим допустимую величину силы 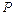 . Используем условие прочности при растяжении и сжатии:
. Используем условие прочности при растяжении и сжатии: 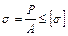 ;
;
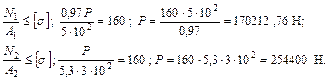
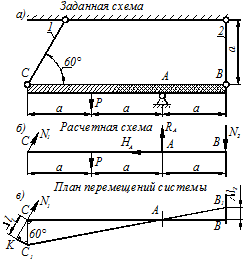
Рисунок 1.10
Итак, допускаемая величина силы 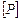 равна меньшей из двух полученных выше сил
равна меньшей из двух полученных выше сил
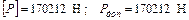
5. Определим напряжения в стержнях
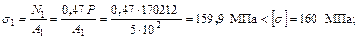
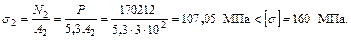
6. Вычислим допускаемую нагрузку по предельному состоянию системы. Предельные усилия в стержнях по пределу текучести:
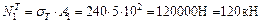 ;
;
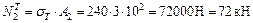 ;
;
Значения 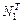 и
и  подставим в уравнение I для определения предельной грузоподъемности
подставим в уравнение I для определения предельной грузоподъемности
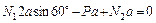 ;
;
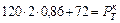 ;
;  ;
;
Допускаемая нагрузка равна:
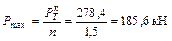
Сравнивая 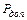 , полученное по допускаемым напряжениям и
, полученное по допускаемым напряжениям и 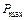 полученное по предельному состоянию видно, что:
полученное по предельному состоянию видно, что:
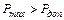 на 15,4 кН, т.е. на 8,99 %.
на 15,4 кН, т.е. на 8,99 %.
Задача 1.5
Для бруса с жестко закрепленными обоими концами рисунок 1.11, определить реакции заделок, построить эпюры продольных сил и нормальных напряжений. Брус состоит из двух участков: первый участок – стальной 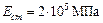 ; второй участок – медный
; второй участок – медный 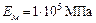 .
.
Решение
1. Статическая сторона задачи
Задача один раз статически неопределима
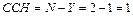
Под действием внешней силы возникают опорные реакции 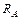 и
и 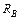
Статика дает одно уравнение с двумя неизвестными
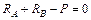 (1)
(1)
Отбрасывая нижнее закрепление, заменяем его действие неизвестной реакцией 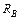 . Таким образом, получим статически определимый брус, нагруженный силами
. Таким образом, получим статически определимый брус, нагруженный силами 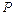 и
и 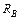 (рис. 1.11 б)
(рис. 1.11 б)
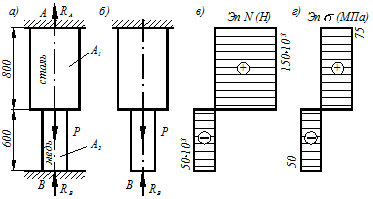
Рисунок 1.11
2. Геометрическая сторона задачи
Так как концы стержня жестко закреплены, то его общая длина не изменится.
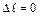 ;
; 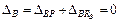 (2)
(2)
3. Физическая сторона задачи
Определим перемещение сечения 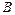 от известной внешней силы
от известной внешней силы 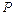
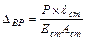 (3)
(3)
Составим выражение для перемещения сечения 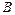 от неизвестной силы
от неизвестной силы 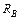
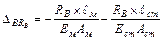 (3)
(3)
4. Синтез
Подставляя выражения (3) и (4) в уравнение (2) получим:
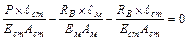 ;
;
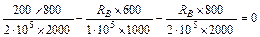 .
.
Откуда 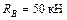 . Подставляя значение
. Подставляя значение 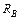 в уравнение (1), получим:
в уравнение (1), получим:
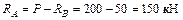 .
.
Эпюра продольных сил представлена на (рис. 1.9 в).
Определим напряжения на участках
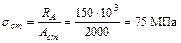 ;
;
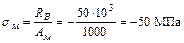 ;
;
Эпюра нормальных напряжений представлена на (рис. 1.11 г). Знак минус поставлен потому, что продольная сила и напряжение сжимающее.
Температурные и монтажные напряжения
Задача 1.6
Стержень постоянного поперечного сечения, жестко закреплен обоими концами в неподвижных опорах (рис. 1.12 а). Часть длиной 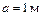 – медная, вторая часть
– медная, вторая часть 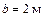 – стальная. После защемления стержня его температура повышается на
– стальная. После защемления стержня его температура повышается на 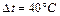 . Коэффициенты температурного расширения:
. Коэффициенты температурного расширения:
стали 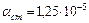 ; меди
; меди 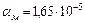 .
.
Определить напряжение в стержне.
Решение
При нагреве стержня он расширяется, и в закреплениях возникают опорные реакции 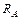 и
и 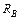 (рис. 1.12 б). Их величину нельзя определить из условий статики. Статика дает одно уравнение с двумя неизвестными:
(рис. 1.12 б). Их величину нельзя определить из условий статики. Статика дает одно уравнение с двумя неизвестными:
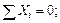
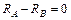 ;
; 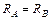
Задача статически неопределима. Для составления дополнительного уравнения учтем, что длина стержня  не изменяется после нагрева.
не изменяется после нагрева.
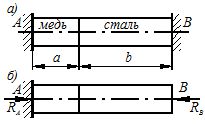
Рисунок 1.12
Ход решения этой задачи аналогичен решению задачи 1.5.
Отбрасываем правую заделку и заменяем ее действие на стержень реактивной силой 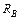 .
.
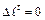 ;
; 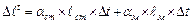 ;
;
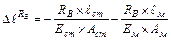 ;
;
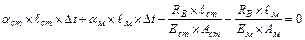 ;
;

Учитывая, что 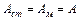 решая уравнение относительно
решая уравнение относительно 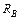 , получим:
, получим:
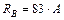 ,
,
тогда напряжение в поперечном сечении стержня равно:
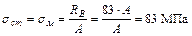
Задача 1.7
Стальной стержень, показанный на рисунке 1.13, состоит из двух частей длиной 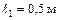 и
и 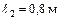 , и площадью поперечного сечения соответственно
, и площадью поперечного сечения соответственно 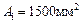 и
и 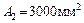 , защемленной одним концом, другой конец не доходит до опоры на величину
, защемленной одним концом, другой конец не доходит до опоры на величину 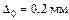 . Найти напряжения в обеих частях стержня при повышении температуры
. Найти напряжения в обеих частях стержня при повышении температуры 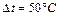 ,
, 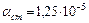 .
.
Решение
Задача статически неопределима. Величину силы 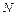 нельзя определить из условий статики.
нельзя определить из условий статики.
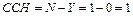
Повышение температуры вызывает удлинение стержня на величину 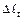 , а его сжатие силами реакций
, а его сжатие силами реакций 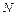 – укорочение на величину
– укорочение на величину 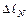 . Абсолютная разность этих деформаций равна величине
. Абсолютная разность этих деформаций равна величине 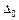 (рис. 1.13)
(рис. 1.13)
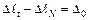
Это уравнение называют условием совместности деформаций:
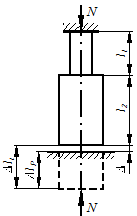 Рисунок 1.13
Рисунок 1.13
| Величины 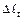 и и 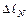 соответственно равны: соответственно равны:
 ; ;
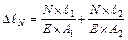 Подставляя в уравнение совместности деформации, полученные выражения величин
Подставляя в уравнение совместности деформации, полученные выражения величин 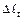 и и 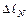 , определим значение силы , определим значение силы 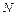 : :
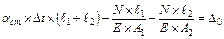 ; ;
|
Искомые напряжения в обеих частях стержня определяются выражением:
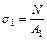 ;
; 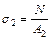
Задача 1.8
Для схемы показанной на рисунке 1.14 а, определить напряжения, возникающие в поперечных сечениях стержней, поддерживающих абсолютно жесткую балку, при нагреве среднего медного стержня на 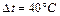 .
.
Принять 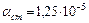 ;
; 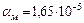 ;
; 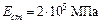 ;
; 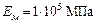 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1340; Нарушение авторских прав?; Мы поможем в написании вашей работы!