Для неравнобокого уголка 1 страница

– из сортамента.

По определяют 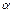(любым способом).

;

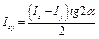
2.11 Знак центробежного момента

В зависимости от расположения уголка, знак центробежного момента инерции можно принять по схеме (рис. 2.3)

Рисунок 2.3

2.12 Моменты инерции простых фигур относительно центральных осей

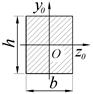
	Прямоугольник ;
	Треугольник

	Круг
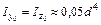
	Кольцо ;

2.13 Вычисление геометрических характеристик плоских сечений

Задача 2.1

Для поперечного сечения состоящего из прокатных профилей (схемы сечений показаны на рис. 2.4) вычислить геометрические характеристики. Данные взять из таблицы 2.5.

Порядок расчета

1. Определить положение центра тяжести сечения.

2. Вычислить осевые и центробежный моменты инерции относительно центральных осей.

3. Определить направление главных центральных осей сечения.

4. Вычислить главные моменты инерции.

5. Вычислить радиусы инерции сечения.

Сечение вычерчивать в масштабе 1:2 с указанием на нем всех осей и размеров, необходимых для выполнения расчета.

Пример расчета задачи 2.1

Дано: Полоса 20 ´ 2; Двутавр № 22 а; Уголок равнобокий 125´10 (рис. 2.6)

Рисунок 2.4

Таблица 2.5

№ п/п	Тип сечения	Двутавр ГОСТ 8239-72	Швеллер ГОСТ 8240-72	Неравнополочный уголок ГОСТ 8510-72
	I			90´56´8
	II			75´50´8
	III			100´63´10
	IV			100´63´6
	V			110´70´6
	VI			125´80´10
	VII			140´90´10
	VIII			160´100´10
	IX	18 а		180´110´10
	X			125´80´12
	е	д	г	е

1. Выпишем данные прокатных профилей из таблицы сортаментов

Полоса 20 ´ 2	Двутавр №22а	Уголок L 125´125´10

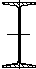
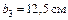
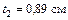
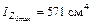
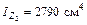
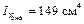
2 Определим координаты центра тяжести заданного сечения по формулам

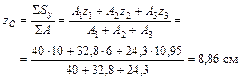
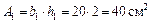
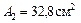
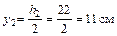
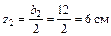
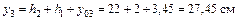
3 Определяем осевой и центробежный моменты инерции каждой фигуры относительно своих центральный осей.

;	;	;
;	;	.

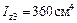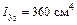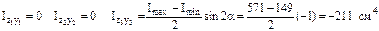
(для неравнобокого уголка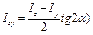

4 Определим осевой и центробежный моменты инерции заданного сечения относительно центральных (случайных) координатных осей и .

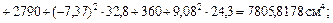
Рисунок 2.6

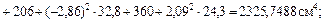
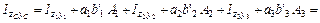
Определим расстояние между параллельными осями

;

;

;

;

;

.

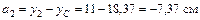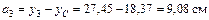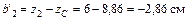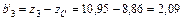5 Определим положение главных осей инерции

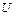отсюда: или (оси и главные)

6. Определим значения главных моментов инерции

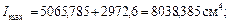
Проверка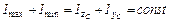

;

7 Определим радиусы инерции сечения

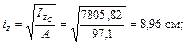
8 Определим осевой момент сопротивления

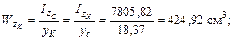
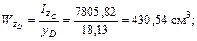
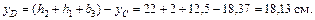
2.14 Вопросы для самопроверки

1. Что называется статическим моментом площади сечения относительно оси?

2. Что называется осевым, полярным и центробежным моментами инерции сечения?

3. Какую размерность имеют моменты инерции сечения?

4. Какая зависимость существует между статическим и моментами относительно двух параллельных осей?

5. Чему равен статический момент относительно оси, проходящей через центр тяжести сечения?

6. Как определяются координаты центра тяжести простого и сложного сечений?

7. Чему равна сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей?

8. Чему равны осевые и полярные моменты инерции круга и кольца относительно их центров?

9. Какие оси называются главными осями инерции?

10. Что представляют собой главные и главные центральные моменты инерции?

11. Чему равен центробежный момент инерции относительно главных осей инерции?

12. В каких случаях без вычисления можно установить положение главных осей?

13. Если 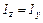и , то какие оси являются главными осями инерции?

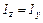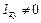14. Если и , то какие оси являются главными осями инерции?

15. Какие центральные оси являются главными осями инерции у сечений, имеющих более двух осей симметрии? Почему?

16. Изменяется ли сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при повороте этих осей?

17. Что называется моментом сопротивления сечения? Его размерность. Радиусами инерции сечения? Их размерность.

18. Чему равны моменты инерции простейших фигур?

19. Как изменится осевой момент инерции при параллельном переносе осей?

Как изменится осевой момент инерции при повороте осей относительно начала координат?

3 КРУЧЕНИЕ

3.1 Общие замечания

При работе бруса на кручение в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент .

Стержни, работающие на кручение, называются валами.

При кручении стержня круглого поперечного сечения, в поперечном сечении возникают касательные напряжения, которые распределены неравномерно, изменяясь по линейному закону – от нуля на оси до максимального значения у поверхности стержня. В связи с этим возникла мысль о замене сплошного вала полым, материал сечения которого находится в более напряженной зоне и используется рациональнее.

Условие прочности при кручении бруса круглого (сплошного или кольцевого) поперечного сечения.

,

где 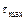– наибольшее касательное напряжение, возникающее в опасном сечении бруса, МПа;

– крутящий момент в опасном сечении бруса, Нм;

– допускаемое касательное напряжение при кручении, МПа;

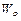– полярный момент сопротивления сечения:

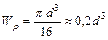– для круглого сечения, м³, см³, мм³;

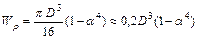– для кольцевого сечения, см³, мм³;

Здесь 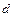– диаметр сплошного сечения;

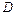и – соответственно наружный и внутренний диаметры кольца;

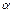– коэффициент, определяемый выражением: .

Условие жесткости при кручении имеет вид:

; ;

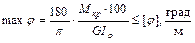– жесткость поперечного сечения при кручении;

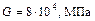– модуль упругости второго рода, модуль сдвига;

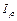– полярный момент инерции сечения, см⁴:

Круг	Кольцо
;	; ;

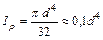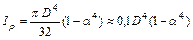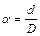При определении диаметра вала из условий прочности и жесткости, из найденных двух значений диаметра выбирается большее и округляется до ближайшего бóльшего стандартного значения.

Обычно при расчете валов зачастую бывают заданы передаваемая мощность (кВт или л.с.) и угловая скорость (с^-1) или 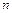(в мин^-1).

Передаваемый валом, вращающий момент, определяется по одной из следующих формул:

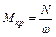, Нм, где 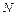– Вт; – с^-1;

или

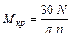, Нм, где 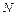– Вт; 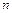– мин^-1.

В старых изданиях встречаются несистемные единицы измерения, использование которых запрещено. Для перевода этих величин в систему измерений SI можно использовать перевод, например:

1 л.с. = 735,499 Вт. Термин лошадиная сила (horse power) была введена Дж. Уаттом для сравнения работоспособности парового двигателя и лошади.

Задача 3.1

К стальному валу приложены три известных момента: , , 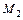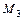(рис.3.1).

Требуется:

1. Установить при каком значении момента , угол поворота правого концевого сечения вала равен нулю;

2. Для найденного значения построить эпюру крутящих моментов;

3. При заданном значении определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей до целого четного числа;

4. Построить эпюру углов закручивания;

5. Найти наибольший относительный угол закручивания (на 1 пог. м).

Данные взять из таблицы 3.1.

Пример расчета задачи 3.1

Дано: = 1900 Нм; 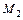= 1200 Нм; 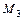= 1100 Нм; а = 1,9 м,
b = 1,2 м, с = 1,1 м, G = 8×10⁴ МПа, [ t ] = 70 МПа

Определить: d, q.

1. Разбиваем заданную схему на участки (рис. 3.2 а).

2. Определим при каком значении момента Х угол поворота правого концевого сечения В равен нулю:

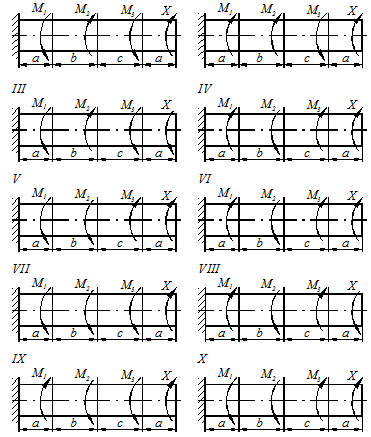
Рисунок 3.1

I

Таблица 3.1

№ п/п	Схема по рис. 3.1	Расстояния, м	Моменты, кНм	, МПа
a	b	c
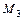
	I		1,2
	II		1,4	1,5
	III		1,5
	I			2,5
	IV	2,5		1,5
	X	1,5		1,2
	IX		1,5
	VIII		1,2	1,5
	VII		1,6	2,5
	VI	1,5	2,5
	е	г	д	г	д	е	д	е

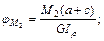
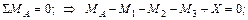II

Проверка

;

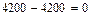
Направление момента Х, показано на рис. 3.2 а.

х

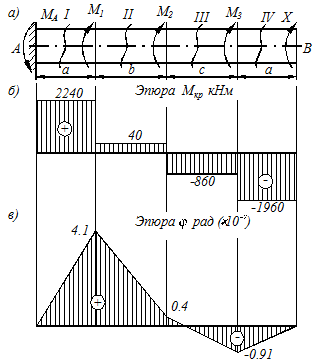
Рисунок 3.2

3. Определим величины крутящих моментов на участках:

Участок I

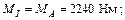
Участок II

Участок III

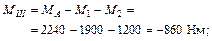
Участок IV

По полученным данным строим эпюру крутящих моментов (рис.3.2 б).

4. Определим диаметр вала, используя условие прочности при кручении:

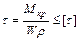
Полярный момент сопротивления равен

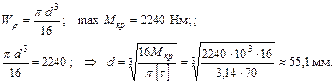
Округляя, принимаем диаметр вала

5. Определим углы закручивания вала на каждом участке

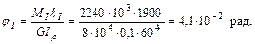
где ,

По полученным данным строим эпюру углов закручивания (рис.3.2 в).

6. Определим максимальный относительный угол закручивания

;

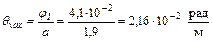Задача 3.2

Для заданного стального вала (рис.3.3) требуется по условию прочности при кручении определить диаметр вала и угол закручивания его конца

Дано: = 6,5 кНм; 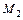= 5,5 кНм; а = 1 м; b = 2 м;

G = 8×10⁴ МПа; [ t ] = 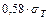= 130 МПа; .

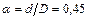Рисунок 3.3

Определим величину крутящих моментов на участках (рис. 3.3 б).

Участок I

;

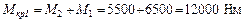Участок II

;

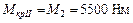Участок III

;

Участок IV

;

По полученным данным строим эпюру крутящих моментов (рис. 3.3 в).

Определим сечение вала по условию прочности при кручении

;

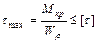Участок сплошного вала I – III

;

; .

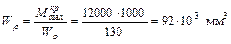Принимаем .

Участок полого вала III – IV

; ;

.

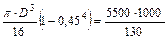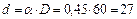Принимаем наружный диаметр мм, тогда внутренний диаметр мм.

Определим угол закручивания конца вала. Угол закручивания свободного конца вала вызывается действием крутящих моментов и .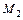

;

;

;

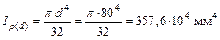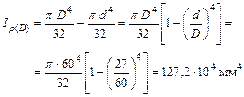Дата добавления: 2014-12-27