Идеальный и реальные газы. Основные газовые законы

Как отмечалось, идеальным называется газ, силы взаимодействия между частицами которого пренебрежимо малы. Уравнение состояния такого газа – уравнение Менделеева – Клапейрона (1.4).

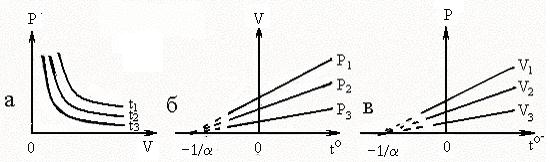
Рис.1. Изменение параметров состояния газа при изотермическом,

изобарном, изохорном процессах

Широко известные газовые законы Бойля – Мариотта и Гей – Люссака – частные случаи уравнения состояния, когда один из параметров состояния остаётся постоянным.

Например, закон Бойля – Мариотта гласит, что для данной массы газа при постоянной температуре (изотермический процесс) давление газа изменяется обратно пропорционально его объёму

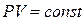(при t°=const) (1.19)

Совокупность состояний, отвечающих одной и той же температуре, изобразится на диаграмме (P, V) гиперболой, определяемой уравнением (1.19), рис.1а.

Закон Гей – Люссака гласит, что при неизменном давлении объём данной массы газа меняется линейно с температурой (аналогично меняется давление при неизменном объёме).

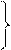
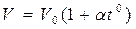при P = const

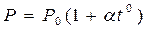при V = const (1.20)

Здесь t⁰ – температура по шкале Цельсия, 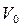– объём при 0° С, 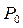– давление при 0° С, коэффициент 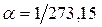, 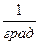. Изобары и изохоры, отвечающие (1.20), показаны на рис. 1б и 1в.

Из уравнения (1.20) следует, что изобары и изохоры пересекают ось t° в одной и той же точке, определяемой условием:

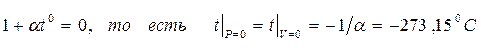
Сместив начало отсчёта температур в эту точку, можно перейти к другой температурной шкале, которую называют абсолютной (или шкалой Кельвина). Между абсолютной температурой, которую принято обозначать Т, и температурой по Цельсию t⁰, имеет место соотношение

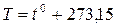(1.21)

С точностью до 0,05% в практических расчётах за абсолютный ноль часто принимают температуру -273° С.

Следует пометить, что выше соотношения (1.19) и (1.20) рассматриваются как частные случаи уравнения состояния (1.4). В действительности, уравнение (1.4) получено как обобщение уравнений (1.19) и (1.20).

Перейдём к количественному определению газовой постоянной R, называемой универсальной газовой постоянной, в уравнении Менделеева – Клапейрона (1.6). Предварительно необходимо дать определение понятий килограмм – молекула и грамм – молекула.

Такое количество данного вещества, масса которого, выраженная в килограммах, численно равна его молекулярному весу, называется килограмм – молекулой или просто киломоль (обозначается кмоль).

Ранее в CGS – системе вместо килограмм – молекулы пользовались грамм – молекулой (или кратко молем), при этом грамм – молекула – такое количество вещества, масса которого, выраженная в граммах, численно равна его молекулярному весу.

В соответствии с законом, установленным Авогадро, киломоли любых газов занимают при одинаковых условиях, то есть при одинаковых температуре и давлении, одинаковый объём. Так при температуре 0° С и давлении 1 атм., называемых нормальными условиями, объём киломоля любого газа равен 22,4 м3/кмоль (аналогично объём моля любого газа равен 22,4 л/моль).

Киломоли и моли всех веществ содержат следующее число молекул: 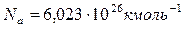, , 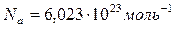где 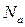– число Авогадро.

Величину универсальной газовой постоянной вычисляют примени-тельно к киломолю вещества, подставляя в соотношение (1.4) давление 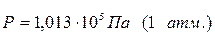, объём V =22,4 м³, температуру Т =273,15 К.

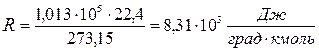
Переходя от киломоля газа к молю и от джоулей к калориям, получают

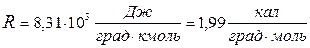
Иногда величину R выражают в литро-атмосферах на град. моль,

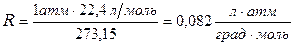
От уравнения состояния для одного киломоля нетрудно перейти к уравнению для любой массы газа m.

Уравнение (1.4) можно записать в виде

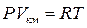, (1.22)

где 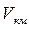– объём одного киломоля.

Объём массы газа m составит 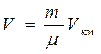, где m – масса киломоля.

Подставляя данное соотношение в (1.20), получаем

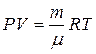(1.23)

Уравнение (1.23) – уравнение состояния для любой массы газа m.

Как отмечалось, идеальный газ представляет собой определённую абстракцию, играющую важную роль при изучении термодинамических процессов. Воздух при обычных, так называемой «комнатной» температуре и атмосферном давлении, близок к идеальному газу. Близки к идеальному газу азот и кислород. Особенно близки по свойствам к идеальному газу гелий и водород. Более того, всякий реальный газ по мере убывания его плотности приближается по своим свойствам к идеальному.

Можно сказать, что поведение реальных газов описывается уравнением (1.23) при не слишком высоких давлениях и обычной температуре. Поясним сказанное на следующем примере. В приближённых расчётах допускается принимать, что радиус молекулы ~ 10^-8 см [3]. При этом объём одной молекулы составит .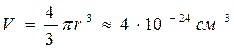

Найдём количество молекул в 1 см3 газа

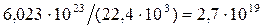
Объём молекул, содержащийся в 1см3газа, составляет

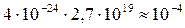см³,

то есть сравнительно небольшую часть объёма 1 см³.

Если газ следовал бы уравнению (1.19), то при повышении давления, например, до 1000 атм. его плотность увеличилась бы в 1000 раз. Объём молекул в 1 см³ составил бы 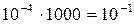см³. Следовательно, на долю молекул приходилось бы 1/10 занимаемого газом объёма, что, несомненно, отразится на характере их движения. При таких условиях обратная пропорциональность объёма давлению должна нарушаться.

Поведение реальных газов описывается уравнением Ван – дер – Ваальса. Оно получено путём введения поправок в уравнение 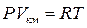и имеет следующий вид

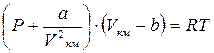, (1.24)

где a, b – константы Ван – дер – Ваальса, имеющие для различных газов свои собственные значения. При необходимости эти константы могут быть определены, например, согласно рекомендациям [3].

В качестве примера в табл. 1 проведено сопоставление значений PV и 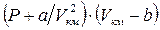для массы азота, занимающей при нормальных условиях (Р₀ = 1 атм., t =0 °C) объём, равный 22,4 литра.

Таблица 1

Дата добавления: 2014-12-27