Теория множеств

Алгебра

СПРАВОЧНЫЙ МАТЕРИАЛ

Теория множеств является основой современной математики. Она возникла в конце XIX века в связи с необходимостью обоснования ряда разделов математики. Первые серьёзные работы по теории множеств принадлежат выдающемуся немецкому математику Георгу Кантору.

Понятия множества является одним из первичных математических понятий и определению не подлежит, его можно описать. Множество есть собрание, совокупность, коллекция объектов, объединённых по какому-нибудь признаку. Множество считается заданным, если указан какой-нибудь признак, по которому относительно произвольного объекта можно судить, входит он в данное множество или нет.

Примерами множеств могут служить: множество студентов в группе, множество натуральных чисел, множество точек отрезка прямой и т.д.

Объекты, входящие во множество, называются его элементами. Говоря о множестве, мы считаем, что относительно всякого объекта верно одно и только одно из двух: этот объект либо входит в данное множество в качестве его элемента, либо не входит.

Множество обозначают большими буквами латинского алфавита: А,В,С…

Запись 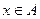означает, что х является элементом множества А. Если х не принадлежит множеству А, то пишут .

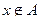Если можно выписать все элементы множества, то записывают

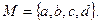
Множество, содержащее конечное число элементов, называют конечным. Например, множество А корней уравнения 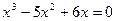содержит только три элемента: 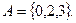К числу конечных множеств относится и пустое множество, то есть множество, не содержащее ни одного элемента. Так, пустым множеством является множество действительных корней уравнения 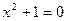. Пустое множество принято обозначать символом 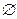. Примером бесконечного множества является множество натуральных чисел.

Множество В является подмножеством множества А, если каждый элемент 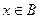является в то же время элементом множества А .

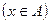Дата добавления: 2014-12-27