Погрешность вычислений

Свойства модуля

1⁰ .

2⁰ .

3⁰ .

4⁰ . ,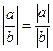

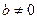
5⁰. .

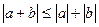При численном решении почти любой математической задачи мы получаем результат с той или иной погрешностью. Отклонение истинного решения задачи от её приближенного решения называется погрешностью решения.

Совокупность всех тех величин, которые нужно задать для получения конкретного решения задачи, называется исходными данными или исходной информацией. Обычно исходные данные получают из эксперимента или из решения другой задачи, поэтому они не истинные, а приближенные. Погрешность решения задачи, возникающую за счёт неточностей исходной информации, называют неустранимой погрешностью.

Для получения численного решения задачи часто приходится её заменять другой аппроксимирующей задачей, которую можно практически решить и решение которой в определённом смысле близко к решению исходной задачи. Погрешность, возникшую при аппроксимации одной задачи другой, называют погрешностью метода.

В процессе численного решения задачи приходится производить округления, заменять иррациональные числа их приближенными значениями. Погрешность, возникшую за счёт самих вычислений, называют вычислительной погрешностью.

Следовательно, полная погрешность решения задачи состоит из неустранимой погрешности, погрешности метода, вычислительной погрешности. Из вышеизложенного ясно, что погрешность метода можно уменьшить за счёт выбора наилучшей аппроксимирующей задачи, вычислительную погрешность можно уменьшить за счёт вычислений с большим количеством разрядов, неустранимую же погрешность изменить нельзя в процессе решения задачи, её можно только оценить.

Остановимся на оценке неустранимой погрешности. Пусть точное значение некоторой величины, 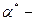её приближенное значение. Предельной абсолютной погрешностью величины 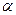называют величину

Предельной относительной погрешностью величины 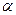называют

Пример. Число .237 округлить до сотых и вычислить его абсолютную и относительную погрешности.

► , ; .◄

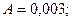
Относительная погрешность обычно выражается в процентах. Она довольно хорошо характеризует приближенные числа, в частности, качество измерений различных величин.

Цифра какого-либо разряда в приближенном числе верна, если это число имеет абсолютную погрешность не больше единицы этого разряда. Если абсолютная погрешность больше единицы какого-либо разряда, то цифра этого разряда и цифры следующих разрядов справа считаются сомнительными.

Запись приближенных чисел производится так, что бы сам вид записи говорил о степени их точности. Обычно их записывают так, что все цифры верны, кроме последней — сомнительной, в которой допускается ошибка не больше единицы. Например, 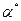= 1,734 значит, что 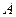= 0,01; т.е. 1,733 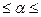1,735. Число знаков после запятой говорит о предельной абсолютной погрешности числа.

Дата добавления: 2014-12-27