Действительные числа

Операции над множествами

Объединение множеств. Объединением двух множеств А и В называется новое множество S, состоящее из всех элементов обоих множеств, причём одинаковые элементы учитываются один раз.

Например, если то

Разность множеств. Разность двух множеств А и В или дополнением множества В до множества А называется множество всех тех элементов множества А, которые не являются элементами множества В.Для разности двух множеств принято обозначение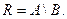

Например, 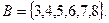Тогда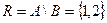

Очевидно,

Пересечение множеств. Пересечением двух множеств А и В есть множество 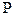, состоящее из всех элементов, общих для обоих множеств. При этом принято обозначение .

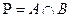Например, 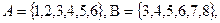тогда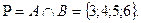

1⁰. Множество чисел 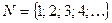называется множеством натуральных чисел.

На множестве натуральных чисел введены операции: сложение, умножение и возведение в натуральную степень.

2⁰. Множество целых чисел .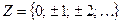

На множестве целых чисел введены операции: сложение, вычитание, умножение и возведение в натуральную степень.

3⁰. Множество рациональных чисел есть множество чисел вида , где 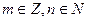, то есть .

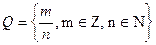Рациональными числами являются числа: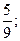

На множестве рациональных чисел введены операции: сложение, вычитание, умножение, деление и возведение в целую степень.

4⁰. Дробь, числитель которой больше или равен знаменателю, называется неправильной. Дробь, числитель которой меньше знаменателя, называется правильной.

Например, дроби — правильные, а дроби — неправильные.

Если дробь неправильная, то ее можно представить в виде суммы целого числа и дроби, то есть смешанным числом. Дробь 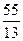— неправильная. (остаток 3). Поэтому .

5⁰. Множество рациональных и иррациональных чисел называется множеством действительных чисел .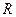

На множестве действительных чисел введены операции: сложение, вычитание, умножение, деление и возведение в рациональную степень.

Примеры иррациональных чисел: .

Стандартный вид положительного действительного числа. Любое положительное число а можно представить в ви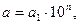де где , а n- целое число, называется порядком числа.

Например, ; .

Для того чтобы положительное число а представить в стандартном виде, нужно поставить запятую так, чтобы в целой части оказалась одна значащая цифра, и умножить полученное число на так, чтобы в результате умножения запятая вернулась на то место, которое она занимала в числе а.

Дата добавления: 2014-12-27