Нахождение параметров линейной регрессии. Нахождение основных числовых характеристик

Нахождение основных числовых характеристик

Ввод данных

Настройка пакета анализа

См. п.1.3.1.

Исходные данные вводятся на рабочий лист пакета Excel (табл. 1.24).

Таблица 1.24 - Исходные данные для получения модели

Чтобы найти основные числовые характеристики, выбираем пункт меню Сервис – Анализ данных – Описательная статистика (см. 1.3.1).

Получается следующая таблица для двухфакторной регрессии (таблица 1.25).

Таблица 1.25 – Основные числовые характеристики

	Y	X1	X2
Среднее	0,584324	102,7027	44,86486
Стандартная ошибка	0,04922	3,479857	3,479274
Медиана	0,58
Мода	0,8
Стандартное отклонение	0,299393	21,16715	21,1636
Дисперсия выборки	0,089636	448,048	447,8979
Эксцесс	-0,00364	-1,0036	-0,85855
Асимметричность	0,50836	0,459765	-0,06146
Интервал	1,1
Минимум	0,1
Максимум	1,2
Сумма	21,62
Счет

Чтобы найти параметры регрессии, выбираем пункт меню Сервис – Анализ данных – Регрессия. Здесь задаем диапазоны отдельно для Y, отдельно – для X (для двухфакторной регрессии в поле «Входной интервал Х» выделяем все значения Х1 и Х2), устанавливаем флажок в окошке «Метки», «Остатки», «Выходной диапазон» – на новый лист. Ок.

Результат получаем в виде нескольких таблиц (1.26…1.29).

Таблица 1.26 – Регрессионная статистика

Множественный R	0,922267101
R-квадрат	0,850576606
Нормированный R-квадрат	0,841786995
Стандартная ошибка	0,119086667
Наблюдения

Таблица 1.27 – Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия		2,744732547	1,372366273	96,77067242	9,2281Е-15
Остаток		0,482175561	0,014181634
Итого		3,226908108

Таблица 1.28 – Коэффициенты модели

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,75088824	0,130300871	-5,762730	1,75Е-06	-1,015692	0,486085
Х1 Х2	0,006869311 0,014035845	0,001015348 0,001015518	6,765475 13,821363	8,88Е-08 1,63Е-15	0,004805 0,011972	0,008933 0,017001

Здесь Множественный R = 0,922, что свидетельствует о тесной взаимосвязи между откликом Y факторами X1, X2. R-квадрат = 0,85 (85%) – значит, общее качество модели хорошее; стандартная ошибка = 0,119.

Значимость F = 9,228E-15 = 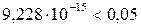, что означает, что полученная модель адекватна по критерию Фишера исходным данным с заданным уровнем доверия. Все дальнейшие расчеты выполняются только при условии адекватности модели.

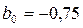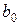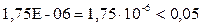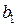Коэффициенты линейной модели , , . Оба коэффициента статистически значимы по критерию Стьюдента, т. к. для P-Значение = , для P-Значение = , для P-Значение = .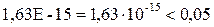

Полученная линейная двухфакторная модель .

Дата добавления: 2014-12-27