Практическое занятие 1

Методические указания к практическим занятиям

Целью практических занятий является закрепление теоретических знаний по основным разделам дисциплины и использование их для получения математических моделей исследуемых процессов резания и режущих инструментов.

Практические занятия охватывают основные разделы дисциплины такие как: оптимизация технических решений; математическое моделирование в экспериментальных исследованиях процессов резания и режущих инструментов; проверка статистических гипотез; статистическое планирование эксперимента; получение зависимостей на основе корреляционного анализа и содержат порядок выполнения работы, варианты индивидуальных заданий, необходимые расчетные формулы и справочные таблицы, контрольные вопросы.

Практическое занятие является завершенным, если качественно выполнены все его разделы, предусмотренные методическими указаниями; выполнены необходимые расчеты; заполнены требуемые таблицы и построены графики; получены математические модели; написаны выводы и сдан зачет по теоретической части.

2 .1 Моделирование процесса резания методом линейного программирования

Цель работы: для заданных условий обработки выбрать оптимальный режим резания, обеспечивающий максимальную производительность механической обработки. Выполнить геометрическую интерпретацию математической модели оптимального режима резания. Исходные данные взять из таблицы 2.1.

Таблица 2.1 – Исходные данные для выбора оптимального режима резания

№ вари-анта	Вид тех-нологи-ческой опера-ции	Обраба-тываемый материал	Станок (мод)	Диаметр до обра-ботки, мм	Диаметр после обра-ботки, мм	Длина обра-ботки	Заданнаяшерохова-тость повер-хности, мм
	точение	Сталь 40Х	1А616				Ra = 3,2
	—//—	Сч 24	16К20				Rz = 40
	—//—	Сч 21	16К20				Ra = 3,2
	—//—	Сталь 45	16К20				Rz = 40
	—//—	Сталь 20	1А616				Rz = 20
	—//—	Сталь 5	16К20				Ra = 2,5
	—//—	Сталь 45	16К20				Rz = 40
	—//—	Сталь 50	16К20				Ra = 3,2
	—//—	Бр АЖ-9-4	1К62				Ra = 2,5
	—//—	Сталь 20ХН	16К20				Rz = 20
	раста-чивание	Сталь 45	16К20				Ra = 3,2
	—//—	Сталь ШХ15	1К62				Rz = 20
	—//—	Сталь 5	16К20				Ra = 3,2
	—//—	Бр АЖ-9-4	16К20				Rz = 6,3
	—//—	Сталь 20ХН	16К20				Ra = 3,2
	—//—	Сч 28	16К20				Rz = 40
	—//—	Сталь 30	16К20				Rz = 80
	—//—	Сч 15	16К20				Ra = 3,5
	—//—	Сталь 40Х	16К20				Rz = 20

Продолжение таблицы 2.1

	—//—	Сталь ХВГ	1А616				Ra = 3,2
	—//—	Сталь 9ХС	1А616				Rz = 20
	—//—	Сталь 50	16К20				Ra = 3,2
	—//—	Сталь 20ХН	16К20				Ra = 3,2
	—//—	Сталь 5	1К62				Rz = 20
	—//—	Сч 36	1К62				Ra = 3,2

2.1.1 Содержание работы

Расчёт оптимального режима резания производят в следующей последовательности:

1 Определяют режущую способность резца, которая выражается скоростью резания

,

Отсюда

, (2.1)

где t – глубина резания, мм;

S – подача, ;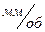

Т – стойкость, мин;

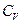– постоянный коэффициент, учитывающий условия обработки;

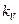– поправочный коэффициент;

m, 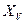, – показатели степени.

2 Определяют эффективную мощность станка

.

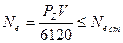где Р_Z – главная составляющая силы резания.

Выразив R_Z и V через D и n получим

,

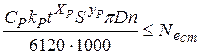отсюда

, (2.2)

где С_Р, k_P – коэффициенты в формуле Р_Z.

3 Определяют допустимую величину шероховатости обработанной поверхности

,

Отсюда

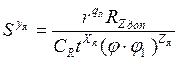, (2.3)

где r –радиус при вершине резца, мм;

φ – главный угол в плане, град;

φ₁ – вспомогательный угол в плане, град;

С_R – постоянный коэффициент, учитывающий условия обработки;

– допустимая высота микронеровностей, мкм.

4 Определяют оптимальную силу, допускаемую прочность слабого звена механизма подачи станка

,

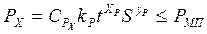Отсюда

. (2.4)

5 Устанавливают следующие ограничения:

– минимальная подача станка 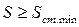, (2.5)

– максимальная подача станка , (2.6)

– минимальная частота вращения шпинделя станка 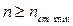, (2.7)

– максимальная частота вращения шпинделя станка 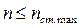, (2.8)

Для того, чтобы производительность 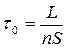была максимальной, т.е. , необходимо чтобы произведение было максимальным.

6 В качестве оценочной принимают функцию

. (2.9)

7 Чтобы систему ограничений и оценочную функцию привести к линейной форме, логарифмируют полученные выражения, предварительно умножив, для удобства вычисления, в первых шести и последнем выражении подачу на 100. Получим

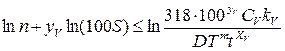; (2.10)

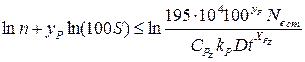; (2.11)

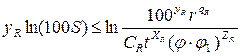; (2.12)

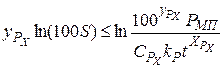; (2.13)

; (2.14)

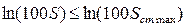; (2.15)

; (2.16)

; (2.17)

. (2.18)

8 Обозначим 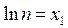, и правые части выражения через b c соответствующими индексами, получим математическую модель оптимального режима резания.

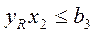
(2.19)

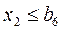
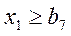
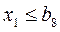
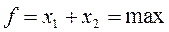. (2.20)

9 Геометрическая интерпретация математической модели представлена на рисунке 1.1. В координатной системе линии 1-УШ соответственно изображают уравнения ограничивающих зависимостей. Штриховой линией 1Х, наклонённой к оси абсцисс под углов 45°, изображена оценочная функция, подлежащая оптимизации. Когда прямая попадёт в точку А многоугольника, линейная форма оценочной функции будет иметь минимальное значение. При дальнейшем перемещении линейная форма будет расти и достигнет максимума в точке С, координаты которой и .

10 Определяют координаты вершины многоугольника, для которой их сумма имеет максимальную величину (.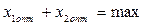

Так как , ,то

, ,

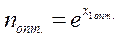где е – основание натурального логарифма.

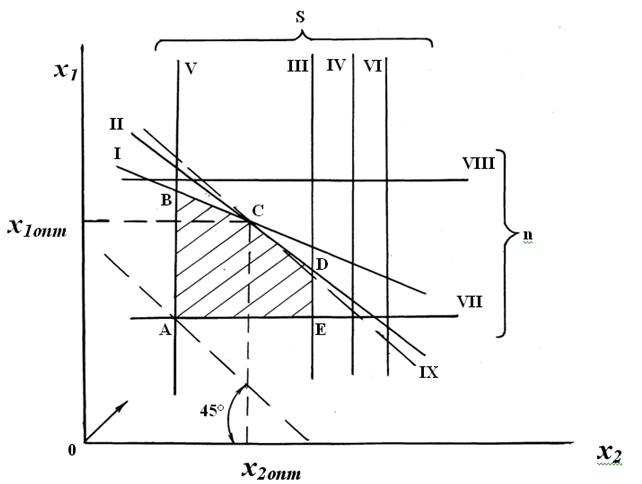
Рисунок 2.1 – Геометрическая интерпретация математической модели оптимального режима резания

2.1.2 Содержание отчёта

1 Название и цель работы.

2 Исходные данные для расчёта оптимального режима резания.

3 Результаты расчёта ограничений.

4 Математическая модель оптимального режима резания.

5 Геометрическая интерпретация математической модели оптимального режима резания.

6 Численные значения оптимального режима резания.

7 Выводы.

2.1.3 Контрольные вопросы

1 Что такое оптимальный режим резания при линейном программировании?

2 Какие ограничения используют при выборе оптимального режима резания?

3 Что принято за оценочную функцию при выборе оптимального режима резания методом линейного программирования?

4 Почему программирование считают линейным?

5 Какие технологические ограничения используют при выборе оптимального режима резания?

6 Как осуществляют геометрическую интерпретацию математической модели оптимального режима резания?

7 Как определяют оптимальные значения элементов режима резания?

Дата добавления: 2014-12-27