
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Excel for Windows. Построение линейной многофакторной модели в приложении
|
|
|
|
Построение линейной многофакторной модели в приложении
Лабораторная работа № 5
Цель работы: по приведенным данным получить линейную модель вида 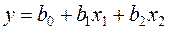 , оценить коэффициенты модели и проверить их значимость по критерию Стьюдента. Проверить полученную модель на адекватность по критерию Фишера. По полученной модели рассчитать значения
, оценить коэффициенты модели и проверить их значимость по критерию Стьюдента. Проверить полученную модель на адекватность по критерию Фишера. По полученной модели рассчитать значения 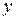 и определить максимальный процент ошибки прогнозирования
и определить максимальный процент ошибки прогнозирования 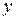 . Исходные данные для получения моделей приведены ниже.
. Исходные данные для получения моделей приведены ниже.
Задача 1. По приведенным ниже данным построить двухфакторную линейную модель зависимости периода стойкости твердосплавных резцов от скорости резания и подачи. Данные получены при точении стали 45 резцами, оснащенными твердым сплавом марки Т15К6 с глубиной t = 2,0 мм. Резец 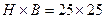 мм,
мм, 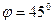 ,
, 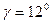 . Критерий отказа – износ по задней поверхности
. Критерий отказа – износ по задней поверхности 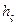 = 0,6 мм.
= 0,6 мм.
| S, мм/об | v, м/мин | |||||||||||
| Т, мин | ||||||||||||
| 0,12 | ||||||||||||
| 0,24 | ||||||||||||
| 0,46 | 3,5 | |||||||||||
Задача 2. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при точении стали резцами 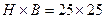 мм, оснащенными пластинами из быстрорежущей стали марки Р9. Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
мм, оснащенными пластинами из быстрорежущей стали марки Р9. Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
| v, м/ мин | Время работы 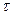 , мин , мин
| ||||||||||||
Износ 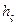 , мм , мм
| |||||||||||||
| 0,08 | 0,13 | 0,16 | 0,21 | 0,25 | 0,28 | 0,32 | 0,35 | 0,40 | 0,43 | 0,47 | 0,52 | 1,00 | |
| 0,12 | 0,17 | 0,23 | 0,27 | 0,32 | 0,37 | 0,41 | 0,46 | 0,53 | 1,00 | ||||
| 0,15 | 0,22 | 0,29 | 0,36 | 0,44 | 0,53 | 1,00 | |||||||
| 0,20 | 0,30 | 0,40 | 0,54 | 1,00 |
Задача 3. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при точении стали резцами 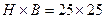 мм, оснащенными пластинами из быстрорежущей стали с покрытием (Р9+TiN). Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
мм, оснащенными пластинами из быстрорежущей стали с покрытием (Р9+TiN). Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
| v, м/ мин | Время работы 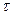 , мин , мин
| |||||||||||||
Износ 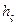 , мм , мм
| ||||||||||||||
| 0,07 | 0,13 | 0,19 | 0,25 | 0,28 | 0,31 | 0,34 | 0,38 | 0,42 | 0,47 | 0,50 | 0,53 | 1,0 | ||
| 0,09 | 0,15 | 0,23 | 0,28 | 0,31 | 0,35 | 0,39 | 0,44 | 0,49 | 0,54 | 1,00 | ||||
| 0,14 | 0,24 | 0,32 | 0,40 | 0,45 | 0,50 | 0,55 | 1,00 | |||||||
| 0,20 | 0,32 | 0,43 | 0,53 | 1,00 | ||||||||||
Задача 4. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа резцов от скорости и времени резания. Данные получены при точении стали 45 резцами 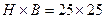 мм. Материал режущей части – Р6М5. Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
мм. Материал режущей части – Р6М5. Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
| v, м/ мин | Время работы 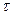 , мин , мин
| |||||||||||
Износ 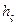 , мм , мм
| ||||||||||||
| 6,5 | 0,15 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | 0,55 | 0,60 | 0,65 | 0,70 | 0,75 | 1,0 |
| 9,0 | 0,20 | 0,35 | 0,42 | 0,49 | 0,56 | 0,65 | 0,68 | 0,75 | 1,00 | |||
| 0,25 | 0,40 | 0,49 | 0,57 | 0,65 | 0,75 | 1,00 | ||||||
| 0,32 | 0,45 | 0,55 | 0,65 | 0,75 | 1,00 |
Задача 5. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа резцов от скорости и времени резания. Данные получены при точении стали 45 резцами 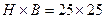 мм. Материал режущей части – (Р6М5+TiN). Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
мм. Материал режущей части – (Р6М5+TiN). Глубина резания t = 2,0 мм, подача s = 0,21 мм/об.
| v, м/ мин | Время работы 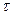 , мин , мин
| ||||||||||||
Износ 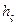 , мм , мм
| |||||||||||||
| 6,5 | 0,22 | 0,30 | 0,37 | 0,45 | 0,48 | 0,52 | 0,56 | 0,60 | 0,63 | 0,67 | 0,71 | 0,75 | 1,0 |
| 9,0 | 0,25 | 0,33 | 0,43 | 0,53 | 0,56 | 0,61 | 0,66 | 0,70 | 0,75 | 1,00 | |||
| 0,30 | 0,40 | 0,50 | 0,60 | 0,65 | 0,70 | 0,75 | 1,00 | ||||||
| 0,33 | 0,45 | 0,56 | 0,68 | 0,75 | 1,00 |
Задача 6. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 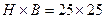 мм. Материал режущей части – Т5К10. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм. Материал режущей части – Т5К10. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 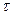 , мин , мин
| ||||||||||||
Износ 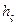 , мм , мм
| |||||||||||||
| 0,10 | 0,17 | 0,22 | 0,28 | 0,34 | 0,41 | 0,47 | 0,54 | 0,60 | 0,67 | 0,73 | 0,8 | 1,2 | |
| 0,12 | 0,20 | 0,28 | 0,35 | 0,42 | 0,50 | 0,58 | 0,68 | 0,80 | 1,20 | ||||
| 0,20 | 0,39 | 0,50 | 0,60 | 0,70 | 0,80 | 1,20 | |||||||
| 0,45 | 0,60 | 0,70 | 0,80 | 1,20 |
Задача 7. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 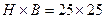 мм, материал режущей части – (Т5К10+TiC). Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части – (Т5К10+TiC). Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 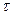 , мин , мин
| ||||||||||||
Износ 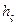 , мм , мм
| |||||||||||||
| 0,10 | 0,20 | 0,30 | 0,40 | 0,45 | 0,50 | 0,55 | 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | 1,20 | |
| 0,12 | 0,23 | 0,35 | 0,46 | 0,51 | 0,57 | 0,63 | 0,69 | 0,74 | 0,80 | 1,20 | |||
| 0,16 | 0,30 | 0,45 | 0,58 | 0,66 | 0,77 | 0,80 | 1,20 | ||||||
| 0,20 | 0,40 | 0,60 | 0,80 | 1,20 |
Задача 8. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструмента от скорости и времени резания. Данные получены при продольном точении стали резцами 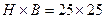 мм, материал режущей части – МС221. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части – МС221. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 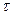 , мин , мин
| ||||||||||||
Износ 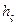 , мм , мм
| |||||||||||||
| 0,12 | 0,20 | 0,27 | 0,32 | 0,37 | 0,41 | 0,46 | 0,51 | 0,56 | 0,62 | 0,68 | 0,80 | 1,2 | |
| 0,15 | 0,22 | 0,30 | 0,36 | 0,42 | 0,48 | 0,54 | 0,60 | 0,67 | 0,80 | 1,20 | |||
| 0,18 | 0,28 | 0,35 | 0,43 | 0,50 | 0,58 | 0,68 | 0,80 | 1,00 | 1,20 | 1,40 | |||
| 0,33 | 0,50 | 0,65 | 0,80 | 1,20 |
Задача 9. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 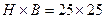 мм. Материал режущей части – МС2215. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм. Материал режущей части – МС2215. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 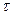 , мин , мин
| ||||||||
Износ 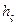 , мм , мм
| |||||||||
| 0,02 | 0,04 | 0,07 | 0,12 | 0,18 | 0,23 | 0,29 | 0,36 | 0,44 | |
| 0,10 | 0,15 | 0,20 | 0,26 | 0,32 | 0,38 | 0,45 | 0,53 | 0,65 | |
| 0,15 | 0,23 | 0,30 | 0,40 | 0,48 | 0,56 | 0,67 | 0,80 | 1,20 | |
| 0,35 | 0,43 | 0,50 | 0,58 | 0,68 | 0,80 | 1,00 | 1,20 | 1,40 |
Задача 10. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 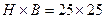 мм, материал режущей части –твердый сплав МС321. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части –твердый сплав МС321. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 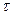 , мин , мин
| ||||||||||||
Износ 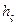 , мм , мм
| |||||||||||||
| 0,07 | 0,13 | 0,19 | 0,25 | 0,32 | 0,38 | 0,44 | 0,50 | 0,56 | 0,62 | 0,68 | 0,75 | 1,2 | |
| 0,09 | 0,15 | 0,23 | 0,30 | 0,38 | 0,45 | 0,52 | 0,60 | 0,67 | 0,75 | 1,20 | |||
| 0,10 | 0,19 | 0,28 | 0,38 | 0,47 | 0,57 | 0,66 | 0,75 | 1,20 | |||||
| 0,20 | 0,38 | 0,58 | 0,75 | 1,20 |
Задача 11. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 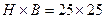 мм, материал режущей части –твердый сплав МС3215. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части –твердый сплав МС3215. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 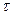 , мин , мин
| ||||||||||||
Износ 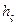 , мм , мм
| |||||||||||||
| 0,09 | 0,18 | 0,28 | 0,37 | 0,42 | 0,47 | 0,51 | 0,56 | 0,60 | 0,65 | 0,70 | 0,75 | 1,2 | |
| 0,11 | 0,23 | 0,35 | 0,46 | 0,52 | 0,57 | 0,63 | 0,69 | 0,75 | 1,20 | ||||
| 0,14 | 0,28 | 0,41 | 0,54 | 0,61 | 0,68 | 0,75 | 1,20 | ||||||
| 0,17 | 0,34 | 0,50 | 0,65 | 0,75 | 1,20 |
Задача 12. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 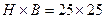 мм, материал режущей части – твердый сплав Т5К10. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части – твердый сплав Т5К10. Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 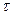 , мин , мин
| ||||||||||||
Износ 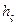 , мм , мм
| |||||||||||||
| 0,27 | 0,33 | 0,39 | 0,45 | 0,48 | 0,54 | 0,60 | 0,65 | 0,70 | 0,77 | 0,87 | 1,0 | 1,5 | |
| 0,32 | 0,40 | 0,47 | 0,55 | 0,63 | 0,70 | 0,80 | 0,90 | 1,00 | 1,50 | ||||
| 0,35 | 0,50 | 0,60 | 0,70 | 0,80 | 0,90 | 1,00 | 1,50 | ||||||
| 0,42 | 0,62 | 0,77 | 0,89 | 1,00 | 1,50 |
Задача 13. По приведенным ниже данным построить двухфакторную линейную модель зависимости износа инструментального материала от скорости и времени резания. Данные получены при продольном точении стали резцами 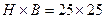 мм, материал режущей части – твердый сплав, подвергнутый виброабразивной обработке (Т5К10+ВО). Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
мм, материал режущей части – твердый сплав, подвергнутый виброабразивной обработке (Т5К10+ВО). Глубина резания t = 3,0 мм, подача s = 0,34 мм/об.
| v, м/ мин | Время работы 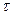 , мин , мин
| ||||||||||||
Износ 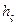 , мм , мм
| |||||||||||||
| 0,12 | 0,25 | 0,37 | 0,50 | 0,56 | 0,62 | 0,69 | 0,75 | 0,81 | 0,88 | 0,94 | 1,00 | 1,5 | |
| 0,15 | 0,30 | 0,46 | 0,61 | 0,69 | 0,77 | 0,85 | 0,91 | 1,00 | 1,50 | ||||
| 0,18 | 0,36 | 0,55 | 0,73 | 0,82 | 0,91 | 1,00 | 1,50 | ||||||
| 0,22 | 0,45 | 0,65 | 0,88 | 1,00 | 1,50 |
Задача 14. По приведенным ниже данным построить двухфакторную линейную модель зависимости прочности твердосплавных резцов (разрушающей подачи 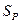 ) от глубины резания t и времени работы на ступени
) от глубины резания t и времени работы на ступени 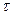 . Данные получены при продольном точении стали 45 резцами
. Данные получены при продольном точении стали 45 резцами 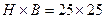 мм, материал режущей части –твердый сплав Т5К10, скорость резания v = 0,3 м/с.
мм, материал режущей части –твердый сплав Т5К10, скорость резания v = 0,3 м/с.
| Глубина резания t, мин | Время работы на ступени 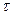 , с , с
| ||||||
Разрушающая подача 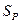 , мм/об , мм/об
| |||||||
| 4,0 | 3,05 | 2,65 | 2,24 | 2,04 | 1,83 | 1,53 | 1,32 |
| 5,0 | 2,65 | 2,24 | 2,04 | 1,83 | 1,53 | 1,32 | 1,12 |
| 6,0 | 2,24 | 2,04 | 1,83 | 1,53 | 1,32 | 1,12 | 1,01 |
Задача 15. По приведенным ниже данным построить двухфакторную линейную модель зависимости прочности твердосплавных резцов (разрушающей подачи 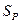 ) от глубины резания t и толщины режущей пластины h. Данные получены при продольном точении стали 45 резцами
) от глубины резания t и толщины режущей пластины h. Данные получены при продольном точении стали 45 резцами 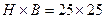 мм, материал режущей части –твердый сплав Т5К10, скорость резания v = 0,3 м/с.
мм, материал режущей части –твердый сплав Т5К10, скорость резания v = 0,3 м/с.
| Толщина пластины h, мм | Время работы на ступени 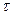 , с , с
| ||||||
Разрушающая подача 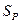 , мм/об , мм/об
| |||||||
| 6,35 | 3,05 | 2,65 | 2,24 | 2,04 | 1,83 | 1,53 | 1,32 |
| 4,76 | 2,65 | 2,24 | 1,83 | 1,53 | 1,32 | 1,12 | 1,01 |
| 3,18 | 1,83 | 1,53 | 1,32 | 1,12 | 1,01 | 0,92 | 0,76 |
Содержание и порядок выполнения работы
Математические модели получают в следующей последовательности (см. 1.3.3):
1 Проверяют установку Пакета анализа в Excel.
2 Вводят исходные данные.
3 Находят основные числовые характеристики.
4 Определяют параметры регрессионной модели. Строят линейную модель 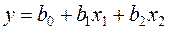 . Определяют тесноту линейной связи по множественному коэффициенту корреляции. Определяют общее качество модели по коэффициенту детерминации
. Определяют тесноту линейной связи по множественному коэффициенту корреляции. Определяют общее качество модели по коэффициенту детерминации 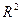 . Проверяют модель на адекватность по критерию Фишера. Все дальнейшие расчеты выполняют только при условии адекватности модели исходным данным. Проверяют статистическую значимость коэффициентов модели. По полученной модели рассчитывают значения показателя y для всех точек выборки.
. Проверяют модель на адекватность по критерию Фишера. Все дальнейшие расчеты выполняют только при условии адекватности модели исходным данным. Проверяют статистическую значимость коэффициентов модели. По полученной модели рассчитывают значения показателя y для всех точек выборки.
5 Используя исходные данные и результаты анализа, делают заключение об адекватности полученной модели и возможности ее использования для прогнозирования.
Содержание отчета
1 Наименование работы.
2 Цель работы.
3 Исходные данные для получения регрессионной модели.
4 Основные числовые характеристики.
5 Коэффициенты регрессионной модели.
6 Уравнение регрессии (математическая модель).
7 Результаты анализа множественного коэффициента корреляции, общего качества модели, адекватности модели и статистической значимости коэффициентов модели.
8 Выводы.
Контрольные вопросы
1 Понятие многофакторной модели.
2 Что характеризует множественный коэффициент корреляции?
3 Назовите последовательность действий для построения многофакторной модели в приложении Excel for Windows.
4 По какому критерию проверяют общее качество модели?
5 Что такое адекватность модели и с помощью какого критерия ее проверяют?
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 853; Нарушение авторских прав?; Мы поможем в написании вашей работы!