Метод Ньютона решения системы нелинейных уравнений

Метод парабол

Если заменить функцию 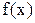на ее трехточечную интерполяцию

(7.17)

то, приравняв ее нулю, получим уравнение

, (7.18)

где

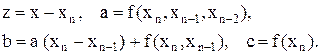(7.19)

Из двух корней уравнения (18) берется наименьший по модулю и следующее приближение принимает значение

. (7.20)

Для начала вычислений необходимо задать три начальных приближения , и (трехшаговый процесс).

Систему нелинейных уравнений можно записать в краткой векторной форме

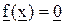(7.21)

или в координатном виде

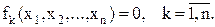(7.22)

Пусть известно некоторое приближение 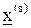к корню . Запишем исходную систему (21) в виде

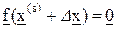, (7.23)

где . (7.24)

Раскладывая уравнения системы (23) в ряды Тейлора с удержанием главных членов приращений, получим СЛАУ

(7.25)

относительно приращений . После ее решения находим новое приближение

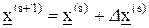. (7.26)

Литература

1. Березин И.С., Жидков Н.П. Методы вычислений: В 2-х томах. - М.: Наука, Физматгиз, 1962.

2. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. - М.-Л.: Наука, Физматгиз, 1963.

3. Воеводин В.В. Численные методы алгебры; теория и алгоритмы. - М.: Наука, 1966.

4. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. - М.: Наука, Гл. ред. ФМЛ, 1972.

5. Калиткин Н.Н. Численные методы. - М.: Наука, Гл. ред. ФМЛ, 1978.

6. Волков Е.А. Численные методы. - М.: Наука, Гл. ред. ФМЛ, 1987.

7. Турчак Л.И. Основы численных методов. - М.: Наука, Гл. ред. ФМЛ, 1987.

8. Коновалов А.Н. Введение в вычислительные методы линейной алгебры. - Новосибирск: ВО Наука, 1993.

9. Григоренко Я.М., Панкратова Н.Д. Обчислювальні методи в задачах прикладної математики. - Київ: Либідь, 1995.

10. Мусіяка В.Г. Основи чисельних методів механіки. - К.: Вища Освіта, 2004.

11. Фельдман Л.П., Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці. - К.: BHV, 2006.

Дата добавления: 2014-12-27