Сложные проценты. Подставляя в формулу (6) известные из условия значения I=1300, n=1/12, i=5%, получим уравнение:

Решение

Решение

Подставляя в формулу (6) известные из условия значения I=1300, n=1/12, i=5%, получим уравнение:

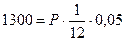
Из данного уравнения найдем величину капитала P=312000 руб.

Пример 8 За какой период времени капитал в $1500 при процентной ставке 2,75% дает процентный доход в $100?

Используем для решения задачи формулу (6). Подставляя P=1500, I=100, i=2,75%, получим уравнение:

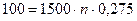
Из данного уравнения находим срок в годах n=0,242424года или 89 дней (результат 88,48 дней округлен в большую сторону).

Сложные проценты - кредитная схема, при которой начисленные проценты присоединяются к основной сумме долга. Т.о. база для начисления сложных процентов увеличивается с каждым периодом выплат.

Формула для расчета наращенной суммы в конце n – го года при условии, что проценты начисляются один раз в году, имеет вид:

S = P(1 + i) ⁿ (12)

Формула (12) называется формулой сложных процентов, а множитель (1 + i) ⁿ называют множителем наращения сложных процентов.

Начисленные за n лет проценты можно рассчитать по следующей формуле:

I = P ((1 + i) ⁿ –1) (13)

При наращении по схеме сложных процентов величина процентов за каждый последующий год увеличивается. Для некоторого промежуточного года t проценты могут быть вычислены по формуле:

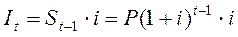, где t=1, 2, …, n.

Необходимо отметить, что основная формула сложных процентов (12) предполагает постоянную процентную ставку на протяжении всего срока начисления процентов. Однако часто используются плавающие или переменные ставки процентов. В этих случаях наращенная сумма рассчитывается следующим образом:

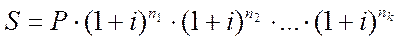(14)

где i_1, i_{2, …,} i_k - последовательные во времени значения процентных ставок;

n₁, n₂,…, n_k – длительность в годах периодов использования соответствующих ставок.

Вычисления по формуле (12) при дробном числе лет довольно затруднительны. Поэтому в тех случаях, когда n не является целым числом, можно использовать следующие формулы:

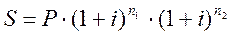, где n = n₁ + n₂ (15)

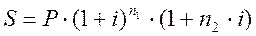, где n = n₁ + n₂ (16)

Заметим, что вычисления по формулам (15) – (16) дают разные результаты: формула (15) дает точное значение наращенной суммы, а формула (16) лишь приближенное.

В методических рекомендациях от 14 октября 1998 года №285-Т рассмотрены следующие варианты начисления сложных процентов[8]:

Пример 9 05.08.98 банк заключает с вкладчиком договор срочного банковского вклада на 21 день (срок возврата вклада - 26.08.98). Сумма вклада - 10 тыс. руб. Процентная ставка - 15%, по условиям договора начисленные по итогам каждого дня срока действия депозита проценты увеличивают сумму вклада.

Дата добавления: 2014-12-27