Решение. a) Вычислим наращенную сумму при ежегодном начислении процентов по формуле (12):

a) Вычислим наращенную сумму при ежегодном начислении процентов по формуле (12):

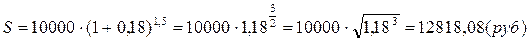
b) Вычислим наращенную сумму при начислении процентов каждые полгода по формуле (17). По условию m=2, тогда:

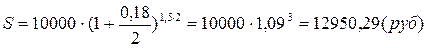
c) Вычислим наращенную сумму при начислении процентов ежеквартально по формуле (17). По условию m=4, тогда:

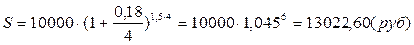
Учитывая, что во всех рассмотренных выше случаях, результат зависит от значения коэффициента наращения, можно для расчета данного коэффициента использовать таблицы множителей наращения из Приложений. Недостатком данных таблиц является то, что их можно использовать только для целого числа периодов начисления и значений приведенных в таблице процентных ставок. Например, для случая b).

b) Число периодов начисления 3 (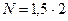), процентная ставка за период – 18%/2=9%.

На пересечении строки с номером 3 и столбца с номером 9% находим значение коэффициента наращения 1,2950. Наращенная сумма составит:

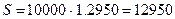руб.

Вывод: Чем чаще идет начисление по схеме сложных процентов, тем больше итоговая сумма.

Формулы (12) и (17) можно также использовать для решения вопросов о вычислении приемлемого размера ставки, определения срока финансовой операции.

В первом случае, выполняя тождественные преобразования уравнения (17) и извлекая корень n-ой степени из обеих частей уравнения, получим:

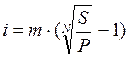(18)

Во втором случае, логарифмируя по какому-либо основанию обе части уравнения (17), получим:

(19)

Полагая в формулах (18) и (19) m=1, можно рассчитать величину ставки сложных процентов и срок операции в годах при ежегодном начислении процентов.

Пример 11 На вклад ежегодно начисляются сложные проценты по ставке 6% годовых. За какой срок первоначальная сумма увеличится в полтора раза?

Дата добавления: 2014-12-27