Непрерывные проценты

Решение

Общая наращенная сумма вычисляется по формуле (25): 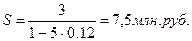Приращение капитала за пять лет составит величину: 7,5-3=4,5 млн.руб.

Приращения за каждый год можно вычислять по формуле (25), несколько видоизменив ее. .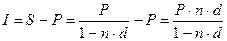

Приращение за первый год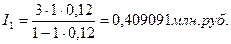

Приращение за второй год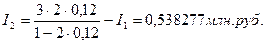

Приращение за третий год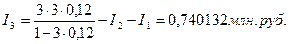

Приращение за четвертый год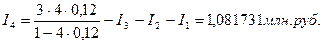

Приращение за пятый год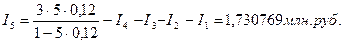

При наращении по простой процентной ставке наращенная сумма составит величину:

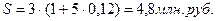
Вывод Наращение по простой учетной ставке дает более значительный рост капитала, чем наращение по простой процентной ставке.

Все рассмотренные ранее методы начисления процентов называются дискретными, т.к. их начисление производилось за фиксированный промежуток времени (год, квартал, месяц). Уменьшая период начисления за счет увеличения частоты начисления процентов, можно перейти к так называемым непрерывным процентам.

Как известно, чем чаще производится начисление процентов, тем быстрее растет наращенная сумма. Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала.

Пусть m – число периодов начисления сложных процентов в году. Из формулы (17) при 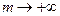следует:

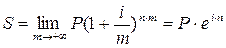, где е ≈ 2,718281. (27)

Чтобы отличить непрерывную ставку от обычной дискретной ставки, вводят специальное обозначение непрерывной ставки δ (дельта) и называют последнюю силой роста. Сила роста показывает скорость относительного роста накапливаемой суммы. Таким образом, формула для нахождения наращенной суммы за n лет при непрерывном начислении процентов примет вид:

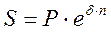. (28)

Пример 18 На сумму 2 тыс. руб. начисляются непрерывные проценты по ставке 8%. Определить наращенную сумму через 5 лет.

Дата добавления: 2014-12-27