Финансовая эквивалентность обязательств

Изменение хозяйственной ситуации нередко побуждает одну из сторон – участниц сделки обратиться к другой стороне с предложением изменить условия ранее заключенных соглашений. Наиболее часто предлагается: заменить одно обязательство другим, например, с более отдаленным сроком платежа, досрочно погасить задолженность, объединить несколько платежей в один (консолидировать платежи) с установлением единого срока погашения и т.п. Естественно, что предлагаемые изменения должны быть безубыточными для обеих сторон. В таких ситуациях неизбежно возникает вопрос о принципе, на котором должно базироваться изменение контракта. Таким общепринятым принципом является финансовая эквивалентность обязательств, которая предполагает неизменность финансовых отношений сторон до и после изменения контракта.

Эквивалентными считаются такие платежи, которые, будучи приведены к одному моменту времени, оказываются равными.

Приведение осуществляется путем дисконтирования на более раннюю дату или, наоборот, наращения суммы платежа, если дата относится к будущему. Если при изменении условий принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить. Две суммы денег S₁ и S₂, выплачиваемые в разные моменты времени, считаются эквивалентными, если их современные (или наращенные) величины, рассчитанные по одной и той же процентной ставке и на одну и ту же дату, одинаковы. Замена S₁ на S₂ в этих условиях формально не изменяет отношения сторон. Поэтому на практике при изменении условий финансовых операций принцип эквивалентности обязательств реализуется путем составления уравнения эквивалентности, согласно которому сумма заменяемых платежей, приведенных к одному моменту времени, приравнивается сумме платежей по новому обязательству, приведенных к тому же моменту времени.

Сравнение платежей предполагает использование некоторой процентной ставки, и, следовательно, результат зависит от выбора ее величины. Однако, что практически весьма важно, такая зависимость не столь жестка, как это может показаться на первый взгляд.

Допустим, что сравниваются два платежа S₁ и S₂ со сроками n ₁ и n₂, измеряемые от одного момента времени, причем S₁ < S₂ и n₁ < n_{2 .} Их современные стоимости P ₁ и P₂ могут быть вычислены для случая простых процентов следующим образом:

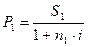
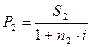
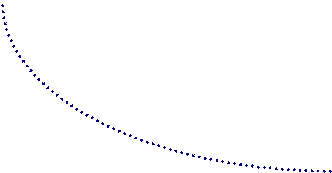
В данных формулах переменная i является аргументом функции, величины P₁ и P₂ – значениями функции. Графиком данной функции будет являться положительная часть гиперболы, т.к. величины i и P не могут быть отрицательными по своему смыслу. С ростом i величина P уменьшается. Зависимость P от i может быть представлена графически:

P

P₁

P₂

0 i₀ i

При i = i₀ наблюдается равенство P₁ = P₂. Для любой ставки i < i₀ P₁ < P₂. В свою очередь, при i > i₀ P₁ > P_2. Таким образом, результат сравнения зависит от критического (барьерного) размера ставки, равного i_{0 .}

Определим величину этой ставки. На основе равенства современных стоимостей сравниваемых платежей получаем уравнение:

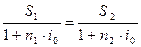
Отсюда находим: 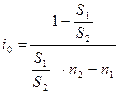(32)

Из этой формулы следует, что чем больше различие в сроках, тем больше величина i₀ при всех прочих равных условиях. Рост отношения S₁/S₂ оказывает противоположное влияние.

Если дисконтирование производится по сложной процентной ставке, то, проводя аналогичные рассуждения, получим формулу для вычисления критического размера ставки сложных процентов:

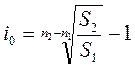(33)

Пример 19 Имеются два обязательства. Условия первого: выплатить 400 тыс руб. через четыре месяца; условия второго: выплатить 450 тыс. руб. через восемь месяцев. Можно ли считать их равноценными?

Дата добавления: 2014-12-27