Общие понятия. Итерационные методы решения СЛАУ

Итерационные методы решения СЛАУ.

Серьезным препятствием при решении систем линейных алгебраических уравнений может оказаться возможность заметного отклонения приближенного значения от точного из-за незначительных возмущений правых частей уравнений, которые возникают в приближенных вычислениях. Например, система

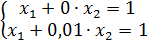
имеет решение: 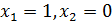или ,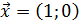

а система

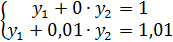
решение: 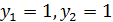или 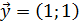. Вторая система отличается от первой лишь небольшим возмущением правой части, которое будет равно

.

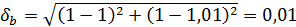При этом возмущение решения будет больше в сто раз

.

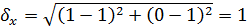Причиной такого нежелательного эффекта может оказаться плохая обусловленность матрицы системы. Параметром оценивающим обусловленность матрицы А системы является число обусловленности матрицы А

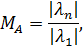
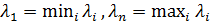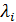где , а – собственные значения[16] матрицы А 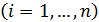. Например, матрица

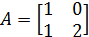
имеет два собственных значения: 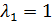и 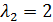. Это легко проверить. Вычислим определитель матрицы А - 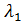Е. Так как матрица

,

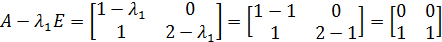то 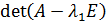определитель будет равен

.

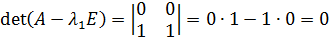Если число обусловленности 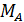большое, то матрицу А и соответствующую ей СЛАУ называют плохо обусловленными.

При этом чем выше порядок системы, тем больше могут оказаться возмущения правой части, а значит и результирующая погрешность.

Подобного недостатка лишены итерационные методы решения СЛАУ. При их применении ответ получается в процессе построения последовательных приближений (итераций) 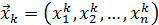, сходящихся к решению системы (1). В итерационной последовательности каждый следующий ее член выражается через предыдущие, уже известные. В частности, в простейшем случае очередной член последовательности 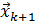может выражаться только через предыдущий 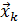. Такие итерационные алгоритмы называются одношаговыми.

При рассмотрении итерационных методов решения СЛАУ ограничимся линейными одношаговыми алгоритмами, которые обычно записывают в стандартной канонической форме

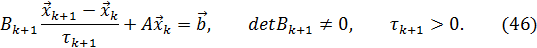
В записи (46) процесс характеризуется последовательностью матриц 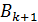и числовых параметров 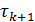, которые называют итерационными параметрами. Если матрицы 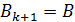и параметры 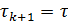не меняются в процессе итераций, т.е. не зависят от индекса k, то итерационный процесс называется стационарным.

Наиболее прост в реализации итерационный процесс с единичной матрицей: . В этом случае из формулы (46) легко получается явное выражение очередной итерации через предыдущую:

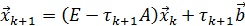, (47)

и итерационный метод (46) решения СЛАУ называют явным. В общем случае, при 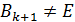, его называют неявным итерационным методом.

Точность итерационного метода (46) характеризуется величиной погрешности

,

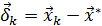где 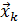– приближенное решение, а 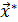– точное решение системы (1). Говорят, что итерационный процесс сходится если

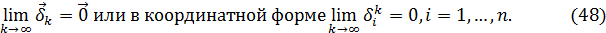
При исследовании сходимости итерационных методов большую роль играют свойства матриц А и 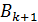, такие как самосопряженность и знакоопределенность.

Определение 1. Матрицы А и А ^* называются самосопряженными, если они связаны операцией транспонирования, т.е.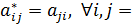

.

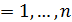Определение 2. Матрица А называется положительно определенной, если для любого отличного от нулевого вектора 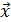справедливо неравенство , т.е. справедливо

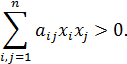
С положительной определенностью матрицы А тесно связано свойство диагонального преобладания:

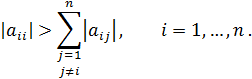
Достаточным условием сходимости любого стационарного итерационного метода является следующая теорема.

Теорема. Пусть А – самосопряженная положительно определенная матрица и выполнено условие

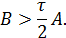
Тогда итерационный процесс (46) сходится, т.е. выполняется условие (48).

Замечание. Метод итерации сходится со скоростью геометрической прогрессии.

При решении СЛАУ итерационными методами обычно задают относительную погрешность 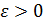, с которой требуется найти приближенное решение 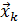, и итерационный процесс прекращают, как только будет выполняться условие

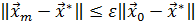, (49)

где 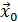– начальное приближение решения, 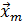– m -ая итерация, 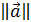– норма вектора . Если m – наименьшее из чисел, для которых выполняется условие (49), то общее число арифметических операций, которые необходимо затратить для нахождения приближенного решения СЛАУ (1), равно 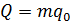, где 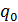– число операций, затрачиваемых для нахождения одной итерации.

Дата добавления: 2014-12-27