Точные (прямые) методы решения СЛАУ

4.1.1. Формулы Крамера [12].

В курсе линейной алгебры решение системы (1) обычно выражают по формулам Крамера в виде отношений двух определителей:

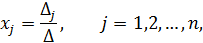
где 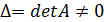, а 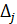, 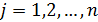– определитель матрицы, полученной из матрицы системы А, заменой j -го столбца столбцом свободных членов , :

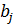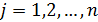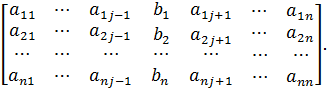
С теоретической точки зрения формулы Крамера дают исчерпывающее решение проблемы. Чтобы найти решение системы (1), нужно подсчитать (n + 1) определитель. Это можно сделать за конечное число арифметических операций. Здесь нас и поджидает основная трудность. Определитель n -го порядка – это n![13] слагаемых, каждое из которых является произведением n чисел. Таким образом, для его вычисления необходимо выполнить 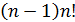умножений и 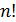сложений, т.е. всего 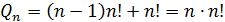арифметических операций. Оценим это число. При достаточно больших 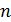, записывается 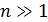, число 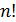можно подсчитать с помощью асимптотической формулы Стирлинга[14]:

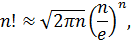
так что

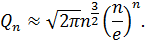
При n = 20 эта формула дает астрономическое число: .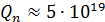

Компьютеру, производительность которого составляет m операций/с, для вычисления определителя 20-го порядка понадобится

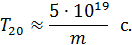
В частности, при m = 10¹⁰ операций/с получим .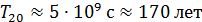

Даже увеличение производительности компьютера на два, три порядка не спасает положения. Такие результаты получены при n = 20, в то время как в современных прикладных задачах приходится решать системы с n = 10⁶ и более уравнений. Из проведенного анализа ясно, что рассчитывать решение СЛАУ по формулам Крамера с вычислением определителей напрямую невозможно, т.е. практическая ценность этих формул невелика.

4.1.2. Метод Гаусса [15].

Выход из критической ситуации, описанной выше, дает метод Гаусса. Этот метод состоит из двух этапов: прямой ход; обратный ход. На первом этапе (прямой ход) система (1) приводится к треугольному виду. Затем на втором этапе (обратный ход) осуществляется последовательное отыскание неизвестных из этой системы треугольного вида.

Перейдем к описанию метода Гаусса. Не ограничивая общность, будем считать, что коэффициент 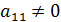(в случае 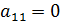поменяем местами 1-ое и i -ое уравнения при условии, что 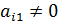; поскольку система предполагается невырожденной, то такой номер i заведомо найдется).

Первый этап (прямой ход).

1 шаг. Исключим из всех уравнений системы (1), кроме первого, неизвестное 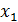. Разделим все члены первого уравнения системы (1) на 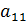и обозначим новые коэффициенты 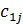, , 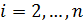а новую правую часть у ₁:

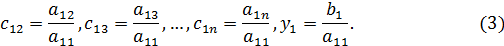
Вычтем из каждого i -го уравнения системы 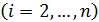преобразованное первое уравнение, умноженное на 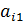. Проделав это, мы исключим неизвестное 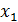из всех уравнений, кроме первого. В результате система (1) примет эквивалентный вид:

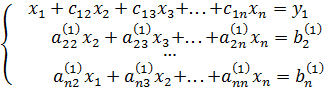. (4)

Значения новых коэффициентов и правых частей системы (4) вычисляются по формулам

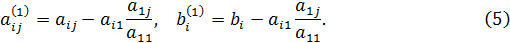
2 шаг. Выделим из (4) «укороченную» систему, содержащую 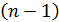уравнение:

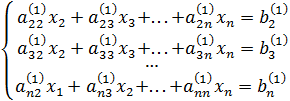. (6)

Разделим все члены первого уравнения системы (6) на 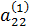и обозначим новые коэффициенты 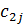, , 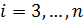а новую правую часть у ₂:

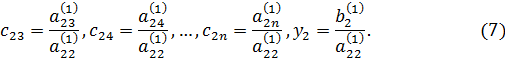
Вычтем из каждого i -го уравнения системы (6) 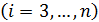преобразованное первое уравнение, умноженное на . Проделав это, мы исключим неизвестное 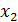из всех уравнений системы (6), кроме первого. В результате система (1) примет эквивалентный вид:

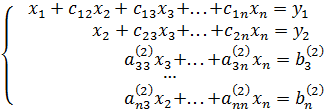. (8)

Значения новых коэффициентов и правых частей системы (8) вычисляются по формулам

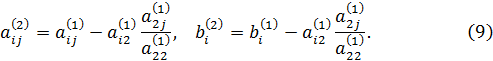
3 шаг. Выделим из (8) «укороченную» систему, содержащую 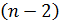уравнение:

. (10)

Исключим из всех уравнений системы (10) кроме первого неизвестное 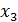и т.д.

Продолжая процесс исключения, после 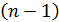-го шага приведем исходную систему (1) к виду

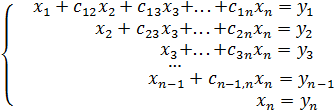(11)

или в матричной форме

.

Матрица С является верхней треугольной матрицей с единицами по главной диагонали:

(12)

Построение системы (11) завершает прямой ход метода Гаусса.

Второй этап (обратный ход).

Обратный ход состоит в последовательном определении неизвестных из системы (11) в обратном порядке, т.е. из последнего уравнения системы (11) выражаем 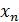, из предпоследнего уравнения системы (11) выражаем 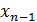и т.д. пока не выразим из первого уравнения 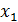. В результате получим эквивалентную (1) систему

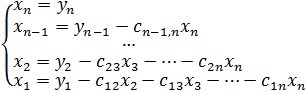(13)

Подсчитаем число арифметических операций, которое требуется выполнить при решении СЛАУ методом Гаусса. Первый шаг прямого хода, согласно формулам (3) и (5), требует n делений и 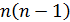сложений и умножений. Второй шаг – 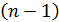делений и 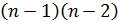сложений и умножений и т.д. В результате общее число арифметических операций на стадии прямого хода включает в себя:

делений

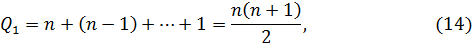
сложений и умножений

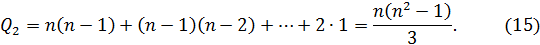
Замечание. Деления учитываются отдельно от сложений и умножений, так как для компьютера это более сложная операция, так же как и для человека.

Обратный ход, согласно формулам, вообще не требует деления, а необходимое число сложений и умножений подсчитывается по формуле

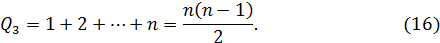
Поэтому общее число арифметических операций, необходимых для решения СЛАУ методом Гаусса равно:

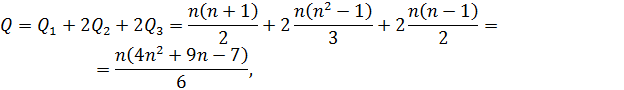
что гораздо меньше числа 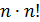, которое требуют формулы Крамера при прямом вычислении определителей.

Пример 1. Решить систему методом Гаусса

Решение.

Прямой ход. 1-ый шаг. Разделим 1-ое уравнение системы на :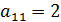

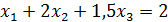. (20)

Умножим уравнение (20) на (−3) и сложим со вторым уравнением системы (18), затем умножим уравнение (20) на (−4) и сложим с третьим уравнением системы (19):

Мы получили систему второго порядка.

2-ой шаг. Разделим уравнение (21) на (−5):

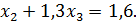(23)

Умножим уравнение (23) на (−3) и сложим с уравнением (22):

(24)

3-ий шаг. Разделим уравнение (24) на (−2,9):

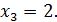
В результате получили систему

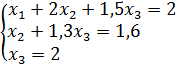(25)

с верхней треугольной матрицей

.

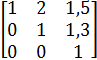Обратный ход. Из системы (25) получаем систему

.

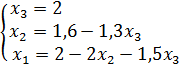Из которой последовательно находим: 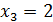, , 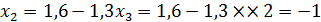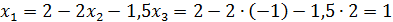. Таким образом, решение системы (17) – (19) найдено: , , .

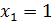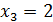Ответ. , , .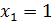

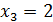Пример 2. Определить число арифметических операций, которое требуется выполнить при решении СЛАУ с тремя неизвестными методом Гаусса.

Решение.

Используем соотношение

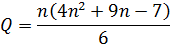
при n = 3. В результате получим, что для решения системы с тремя неизвестными потребуется выполнить

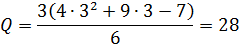
арифметических операций.

Ответ. .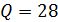

Описанная процедура решения системы (1) методом Гаусса может оказаться неустойчивой по отношению к ошибкам, которые неизбежны при компьютерных вычислениях в результате округления чисел из-за конечной длины машинного слова. Подобные ошибки возникают, если в процессе прямого хода в матрице С (12) образовались большие по абсолютной величине элементы. В этом случае при вычислении неизвестных по формулам (13) в процессе обратного хода умножение найденных с ошибками округления чисел 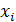на большие по модулю элементы матрицы С приведет к накоплению подобных ошибок.

Для того чтобы нивелировать роль ошибок округления в процессе вычислений используют способ коррекции, который называется выбором ведущего элемента по строке. Он заключается в следующем. Приступая к 1-му шагу прямого хода, рассмотрим элементы 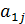первой строки матрицы А и найдем наибольший по модулю. Пусть это – 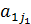. Поменяем в системе (1) первый столбец и столбец с номером j ₁ местами, изменив соответствующим образом нумерацию неизвестных. В результате наибольший по модулю элемент первой строки станет ведущим элементом первого шага 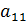. Благодаря этому все элементы 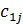первой строки матрицы С, которые рассчитываются по формулам (3), будут удовлетворять условию .

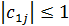Процедуру выделения наибольшего по абсолютной величине элемента в очередной строке и превращения его в ведущий элемент нужно повторять во время каждого шага прямого хода метода Гаусса. В это случае все ненулевые элементы 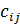матрицы С, будут удовлетворять условию 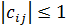, обеспечивая устойчивость метода по отношению к ошибкам округления.

Пример 3. Решить систему методом Гаусса

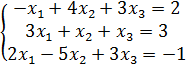(26)

используя способом выбора ведущего элемента по строке.

Решение.

Прямой ход. 1-ый шаг. Выберем ведущий элемент первого шага. Выпишем матрицу системы

.

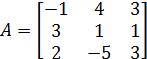Так как наибольший элемент в первой строке матрицы 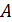равен 4 и это коэффициент при 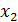, то поменяем местами первый и второй столбцы матрицы. В результате система (26) перепишется в виде:

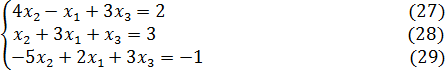
Разделим 1-ое уравнение (27) на :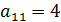

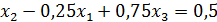. (30)

Умножим уравнение (30) на (−1) и сложим со вторым уравнением (28), затем умножим уравнение (30) на 5 и сложим с третьим уравнением (29):

Мы получили систему второго порядка.

2-ой шаг. Выберем ведущий элемент второго шага. Выпишем матрицу системы (31), (32)

.

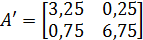Так как наибольший элемент в первой строке матрицы равен 3,25 и это коэффициент стоит в первом столбце, то он и является ведущим элементом строки. Следовательно, никаких перестановок делать не нужно.

Разделим уравнение (31) на 3,25:

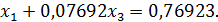(33)

Умножим уравнение (33) на (−0,75) и сложим с уравнением (32):

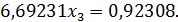(34)

3-ий шаг. Разделим уравнение (34) на 6,69231:

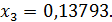
В результате получили систему

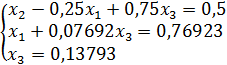(35)

с верхней треугольной матрицей

.

Обратный ход. Из системы (35) получаем систему

.

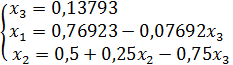Из которой последовательно находим: 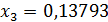, , 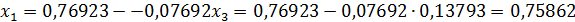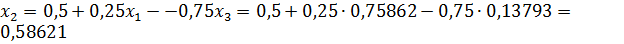. Таким образом, решение системы (26) найдено: , , .

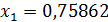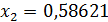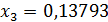Ответ. , , .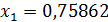

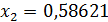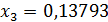Дата добавления: 2014-12-27