Наилучшее среднеквадратическое приближение

До сих пор мы рассматривали построение интерполяционных многочленов 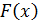, совпадающих со значениями исходной функции 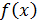на некотором множестве узлов интерполяции :

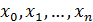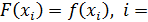
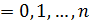. Функция 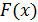приближает (аппроксимирует) функцию 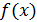на .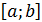

Рассмотрим общую задачу об аппроксимации функции 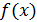функциями из 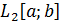, где 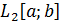– пространство функций действительной переменной со скалярным произведением

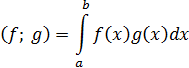
и нормой

.

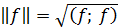Заменим требование 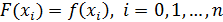условием минимума нормы: 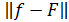или малости нормы 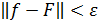, где 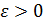– заданная точность.

Отыскание 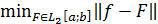есть задача о нахождении наилучшего среднеквадратичного приближения. В качестве 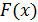возьмем обобщенный многочлен

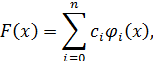
где 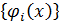– семейство ортонормированных на 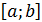функций, т.е. для 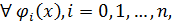выполняется

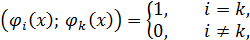
а 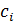– произвольные коэффициенты. Тогда задача нахождения наилучшего среднеквадратичного приближения сводится к отысканию минимума функции 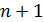-ой переменных :

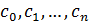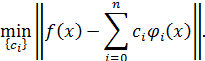
Вычислим среднеквадратичное уклонение

.

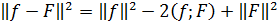Подставляя сюда выражения

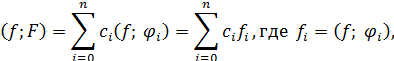
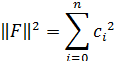
получим

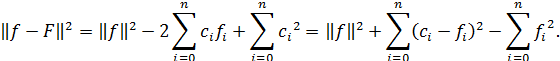
Отсюда видно, что минимум погрешности достигается при 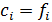, т.е. на функции

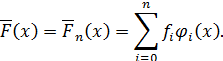
В этом случае среднеквадратичное уклонение

Таким образом, наилучшее среднеквадратичное приближение существует и единственно. Оно приводит к задаче о вычислении интегралов для определения

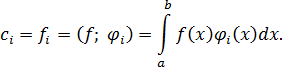
Утверждение. Наилучшее среднеквадратичное приближение сходится к и возможна аппроксимация с любой точностью 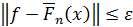, если n достаточно велико, т.е. .

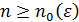Глава 4. Численное решение систем линейных алгебраических уравнений. Численное решение систем нелинейных уравнений.

В этой главе мы рассмотрим одну из самых важных задач линейной алгебры – решение систем линейных алгебраических уравнений (СЛАУ), в которых число уравнений равно числу неизвестных:

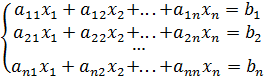(1)

или в сокращенном виде:

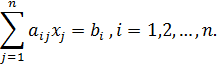
Коэффициенты 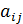при неизвестных 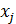образуют матрицу[10] системы (1):

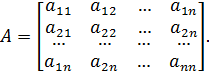(2)

На протяжении этой главы будем считать, что определитель матрицы А отличен от нуля:

.

В этом случае система имеет единственное решение и называется невырожденной. Рассмотрим методы фактического построения этого решения. Выделяют две группы подобных методов: 1) точные (прямые) методы; 2) итерационные методы.

Точными (прямыми) называются методы, которые позволяют получить точное решение невырожденной системы (1) за конечное число операций, если свободные члены 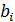и коэффициенты при неизвестных 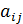заданы точно и вычисления ведутся без округления. Конечно, точные методы также дают решение с определенной точностью, которая зависит от погрешностей округления, т.е. от машины, и от характера вычислительной устойчивости, которая зависит от самого метода.

Итерационные методы позволяют найти приближенное решение путем построения последовательности приближений (итераций), начиная с некоторого начального приближения. Само приближенное решение является результатом вычислений, полученным после конечного числа итераций.

Так же в этой главе мы познакомимся с одним из итерационных методов решения систем нелинейных уравнений, а именно, методом Ньютона.

Дата добавления: 2014-12-27