
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Составим таблицу значений синуса в узлах интерполяции : i
|
|
|
|
Решение.
Составим таблицу значений синуса в узлах интерполяции  :
:
| i | |||
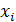
| 
| 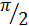
| |
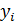
| 
|
Для записи интерполирующего многочлена Лагранжа воспользуемся формулой (8) в ее развернутой форме:
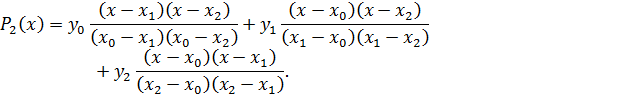
В результате получим

Следовательно, искомый многочлен имеет вид:
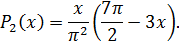
Вычислим значение интерполирующего многочлена в точке 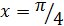 :
:

Теперь сравним полученный результат с точным значением синуса в этой точке:
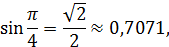

Пример 2. Вычислить, используя интерполяционный многочлен Лагранжа, приближенное значение функции 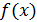 в точке х * = 0,5, если
в точке х * = 0,5, если 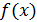 задана таблично
задана таблично
| i | ||||
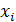
| -1 | |||
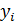
| 0,25 | 0,5 |
Построим интерполяционный многочлен Лагранжа, используя формулу (8). Так как по условию задачи n = 3, то искомый многочлен – многочлен третьей степени:


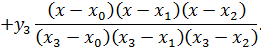
Учитывая табличные значения 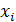 и
и 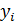 получим:
получим:


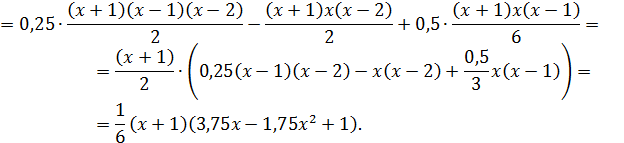
Поэтому искомый многочлен имеет вид:
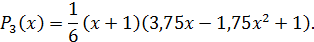
Теперь вычислим значение полученного многочлена в точке х * = 0,5
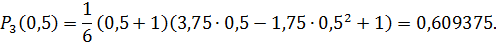
Следовательно,  .
.
Ответ.  .
.
3.1.3. Интерполяционный многочлен в форме Ньютона [9].
Интерполяционный многочлен Лагранжа, несмотря на свое изящество, неудобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь многочлен заново.
Перепишем интерполяционный многочлен Лагранжа в эквивалентной форме:

где 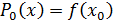 – многочлен нулевой степени, а
– многочлен нулевой степени, а  – многочлен Лагранжа степени
– многочлен Лагранжа степени 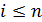 , соответствующий узлам интерполяции
, соответствующий узлам интерполяции  .
.
Обозначим
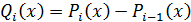 . (9)
. (9)
Многочлен 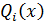 имеет степень i и по построению обращается в ноль при
имеет степень i и по построению обращается в ноль при 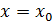 ,
, 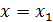 , …,
, …, 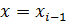 , поэтому его можно представить в виде
, поэтому его можно представить в виде
 ,
,
где Аi – числовой коэффициент при хi. Так как  не содержит степень i, то Аi совпадает с коэффициентом при хi в многочлене
не содержит степень i, то Аi совпадает с коэффициентом при хi в многочлене  . Следовательно, в силу (5) и (7) его можно записать в виде
. Следовательно, в силу (5) и (7) его можно записать в виде

При этом 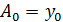 .
.
Формулы (9) и (10) позволяют написать рекуррентное соотношение для многочлена 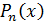 :
:
 . (11)
. (11)
Выражая аналогичным образом по индукции 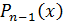 через
через 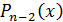 ,
, 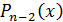 через
через  и т.д., получим окончательное выражение для многочлена
и т.д., получим окончательное выражение для многочлена 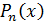 :
:
 . (12)
. (12)
Представление интерполяционного многочлена в виде (12) называется интерполяционным многочленом в форме Ньютона или просто интерполяционным многочленом Ньютона. Это представление удобно тем, что при увеличении n на единицу требуется добавить к «старому» многочлену только одно слагаемое.
Пример 1. Написать интерполяционный многочлен Ньютона для функции 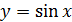 по ее значениям в трех точках
по ее значениям в трех точках 
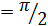 .
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!