Оценка погрешности интерполирования

Замена функции f (x) интерполяционным многочленом 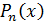приводит к появлению погрешности

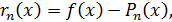
которая называется остаточным членом интерполяционной формулы. Очевидно, что в узлах интерполяции погрешность 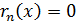, так как 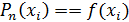, i =0, 1, 2, …, n. Для оценки остаточного члена в иных точках используют соотношение:

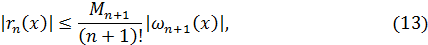
где 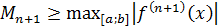, а .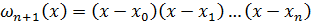

Многочлен 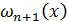на отрезке 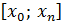имеет n +1 нуль в узлах интерполяции, а его значения между этими нулями сравнительно невелики, но если точка х выходит за пределы отрезка 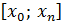и удаляется от точки х ₀ влево или от точки х_n вправо, то оценка (13) ухудшается из-за быстрого роста функции .

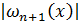Из сказанного можно сделать следующий вывод. Если 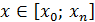, то множитель 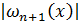не обесценивает оценку (13). Такой случай называют собственно интерполяцией f (x). Противоположный случай, когда 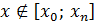называется экстраполяцией функции f (x). Отмеченная выше особенность многочлена 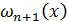резко ухудшает оценку (13) при экстраполяции. Поэтому на практике экстраполяции избегают или ограничиваются многочленами невысокой степени, когда рост функции 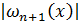не достаточно критичен.

Пример 1. Найти оценку для погрешности (13) при вычислении приближенного значения синуса в точке 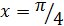с помощью интерполяционного многочлена второй степени . Сравнить ее с погрешностью, подсчитанной непосредственно в примере п. 3.1.2.

Дата добавления: 2014-12-27