Ая итерация

Ая итерация.

Ая итерация.

Ая итерация.

Ая итерация.

Ья итерация.

Ая итерация.

Ая итерация.

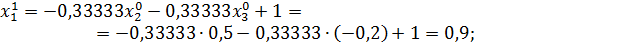
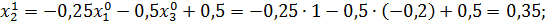
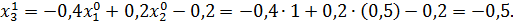
Значит 1-ое приближение равно 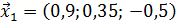. Проверим выполнение условия (56). Так как

,

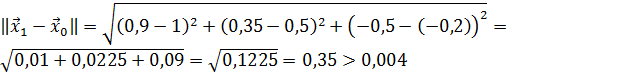то вычисления продолжаем.

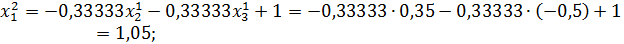
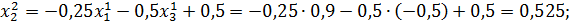
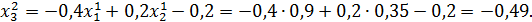
Значит 2-ое приближение равно 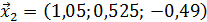. Проверим выполнение условия (56). Так как

,

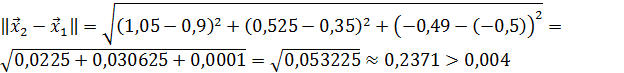то вычисления продолжаем.

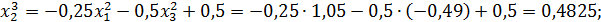
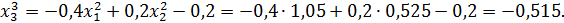
Значит 3-ое приближение равно 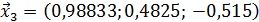. Проверим выполнение условия (56). Так как

,

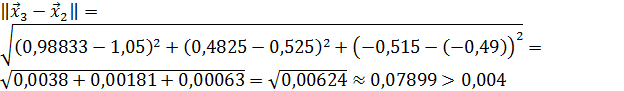то вычисления продолжаем.

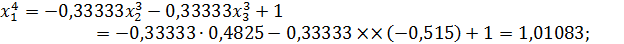
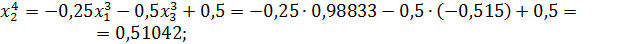
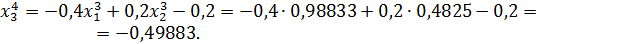
Значит 4-ое приближение равно 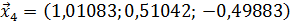. Проверим выполнение условия (56). Так как

,

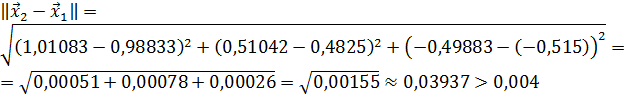то вычисления продолжаем.

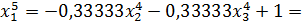
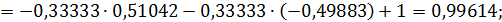
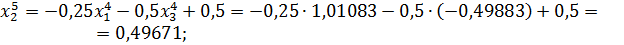
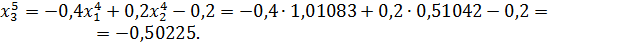
Значит 5-ое приближение равно 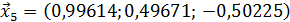. Проверим выполнение условия (56). Так как

,

то вычисления продолжаем.

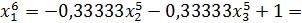
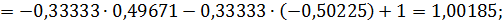
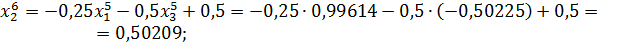
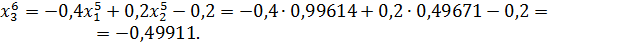
Значит 6-ое приближение равно 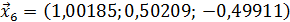. Проверим выполнение условия (56). Так как

,

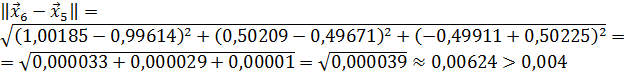то вычисления продолжаем.

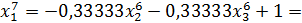
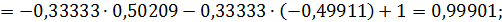
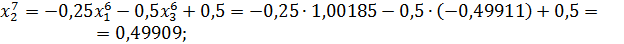
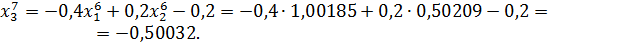
Значит 7-ое приближение равно 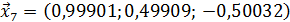. Проверим выполнение условия (56). Так как

,

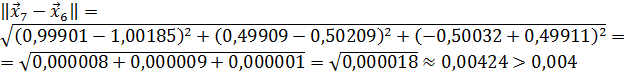то вычисления продолжаем.

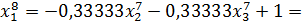
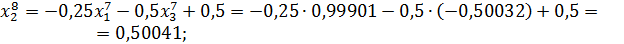
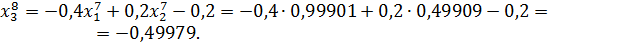
Значит 8-ое приближение равно 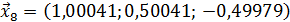. Проверим выполнение условия (56). Так как

,

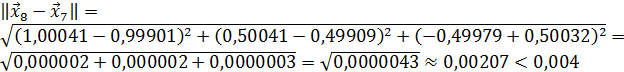то вычисления прекращаем, так как требуемая точность достигнута. Следовательно, искомое решение – 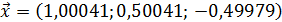с точностью до ε= 0,01.

Ответ. 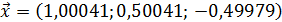с точностью до ε= 0,01.

4.2.3. Метод Зейделя [19].

Рассмотрим каноническую форму записи стационарного итерационного процесса (46). Матрицу

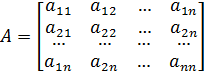
запишем в виде суммы трех матриц:

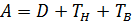, (57)

где 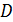– диагональная часть матрицы А, 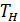– нижняя треугольная матрица, 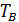– верхняя треугольная матрица, т.е.:

;

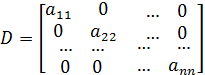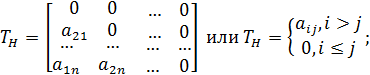
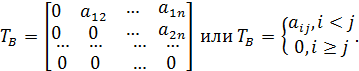
Положим

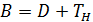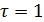, . (58)

В результате формула (46) примет вид

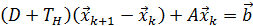
или

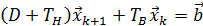. (59)

Так как матрица 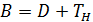, то схема метода Зейделя (59) является неявной. Однако, так как 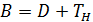– треугольная матрица, то итерация 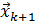находится по явным формулам.

Перепишем рекуррентное соотношение (59) в координатной форме:

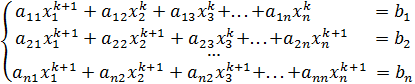. (60)

Уравнения системы (60) позволяют последовательно рассчитать компоненты вектора -ой итерации 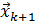подобно тому, как это делалось во время обратного хода в методе Гаусса:

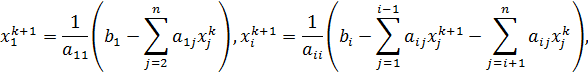
Часто на практике метод Зейделя используют записанным в следующей форме 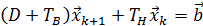, т.е. если матрица 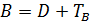. В этом случае из системы (60) для определения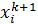 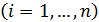получим следующие рекуррентные соотношения:

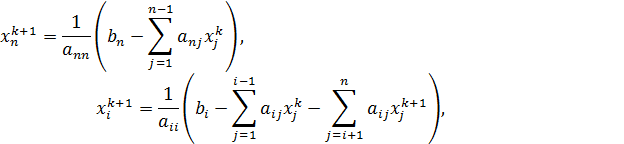
Рассмотрим вопрос сходимости метода Зейделя. Для этого метода справедливо следующее утверждение.

Теорема. Метод Зейделя всегда сходится, если А – самосопряженная положительно определенная матрица.

К утверждению данной теоремы можно добавить и еще одно: метод Зейделя сходится для любой системы, в которой матрица системы А обладает свойством диагонального преобладания.

Если А – симметричная матрица и выполняется

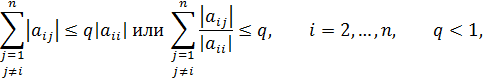
то метод Зейделя сходится со скоростью геометрической прогрессии со знаменателем 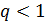. При этом, так же как и в схеме простой итерации, итерационный процесс в методе Зейделя продолжается до момента выполнения неравенства (54).

Пример 1. Методом Зейделя решить с точностью до ε= 0,001 систему линейных алгебраических уравнений:

.

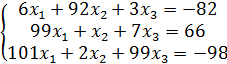Решение. Приведем систему к виду с диагональным преобладанием. Так как 92 > 6 + 3, то в первом уравнении преобладающим будет коэффициент при 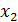, а так как 99 > 1 + 7, то во втором уравнении – при 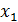. В третьем уравнении коэффициент при 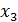будет преобладающим, если из этого уравнения вычесть второе уравнение. Поэтому вычтем из 3-его уравнения 2-ое и поменяем местами 1-ое и 2-ое уравнения системы. В результате чего получим:

.

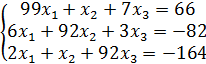Так как данная система – система с диагональным преобладанием, то условие сходимости метода Зейделя выполнено. Учитывая, что

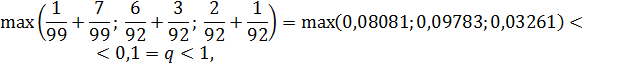
то вычисления будем проводить до момента выполнения неравенства

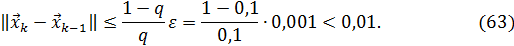
За начальное приближение 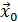возьмем вектор свободных членов 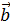, т.е. 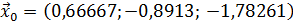, а последовательные приближения будем вычислять по формулам (61). В данном случае имеем:

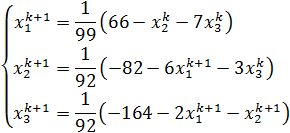
или .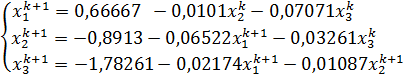

Дата добавления: 2014-12-27