Правило Крамера решения системы n линейных уравнений с n неизвестными

Понятие решения системы линейных уравнений

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ ПО ПРАВИЛУ КРАМЕРА И МЕТОДОМ ГАУССА.

Лекция 4. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

План:

1. Понятие решения системы линейных уравнений.

2. Правило Крамера решения системы n линейных уравнений с n неизвестными.

3. Метод Гаусса решения системлинейных уравнений.

4. Критерий Кронеккера-Капелли совместности систем линейных уравнений.

Рассмотрим систему n линейных уравнений с n неизвестными.

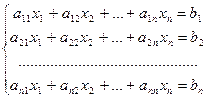
Решением системы называется совокупность чисел (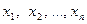), которая обращает каждое уравнение системы в верное равенство.

Система n линейных уравнений с n неизвестными может иметь одно решение, бесчисленное множество решений или не иметь решений вообще.

Если система линейных уравнений имеет хотя бы одно решение, то она называется совместной, если система не имеет решений, то она называется несовместной.

Рассмотрим основные методы решения систем n линейных уравнений с n неизвестными:

· правило Крамера;

· метод Гаусса.

Теорема. Система n линейных уравнений с n неизвестными имеет единственное решение, если определитель, составленный из коэффициентов при неизвестных, отличен от нуля.

Это решение находится по правилу Крамера:

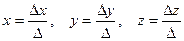
где ∆ – определитель, составленный из коэффициентов при неизвестных;

∆ _х получается из определителя ∆ заменой столбца коэффициентов при x столбцом свободных членов;

∆ _у получается из определителя ∆ заменой столбца коэффициентов при у столбцом свободных членов;

∆ _z получается из определителя ∆ заменой столбца коэффициентов при z столбцом свободных членов.

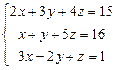
Пример 4.1. Решите систему уравнений по правилу Крамера:

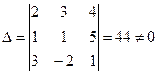Решение. Составим определитель ∆ из коэффициентов при неизвестных и вычислим его:

Определитель ∆ отличен от 0, следовательно, система имеет единственное решение. Для его нахождения вычислим ∆ _х, ∆ _у и ∆ _z:

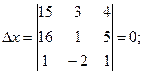
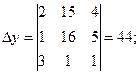
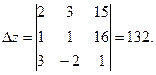
По правилу Крамера найдем неизвестные:

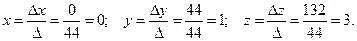
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.

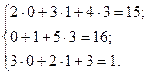Истинно.

Итак, решение системы найдено правильно.

Ответ: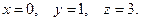

Для нахождения числа решений системы n линейных уравнений с n неизвестными можно использовать следующую блок-схему:

…

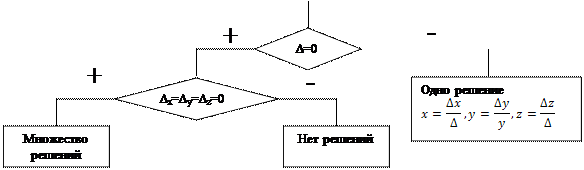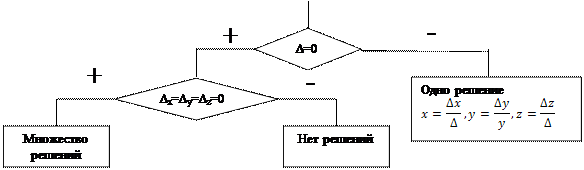Дата добавления: 2014-12-27