Метод Гаусса решения систем линейных уравнений

Метод Гаусса является более универсальным, чем правило Крамера, так как позволяет находить решения в следующих случаях:

1. Число уравнений не равно числу неизвестных.

2. Если в правиле Крамера ∆ = ∆ _х= ∆ _у = ∆ _z= 0.

Введем следующие понятия:

Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы.

Матрица B, состоящая из элементов матрицы А и столбца свободных членов, называется расширенной матрицей.

Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули.

Это достигается с помощью элементарных преобразований матрицы над строками. В результате таких преобразований не нарушается равносильность системы, и она приобретает треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n -ую неизвестную, с помощью обратного хода получают значения всех неизвестных.

Пример 4.2. Решите систему уравнений методом Гаусса:

Решение. Выпишем расширенную матрицу системы и приведем её к треугольному виду: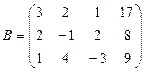

Поменяем местами первую и трелью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных коэффициентов при последующих вычислениях.

Первую строку полученной матрицы умножаем последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:

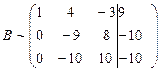
Для упрощения вычислений умножим третью строку на (-0,1) и поменяем ее местами со второй строкой. Тогда получим:

Далее, умножая вторую строку матрицы на 9 и складывая с третьей, окончательно получим:

Восстановим из полученной матрицы В систему уравнений равносильную данной, начиная с последнего уравнения:

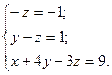
Из последнего уравнения находим: z = 1.

Подставим z = 1 во второе уравнение системы: y – 1 = 1; y = 2.

После подстановки z = 1 и y = 2 в первое уравнение получим: x + 4·2 - 3·1 = 9;

x = 9 – 8 + 3; x = 4. Итак, x = 4, y = 2, z = 1.

Проверка:

Следовательно, решение системы найдено верно.

Ответ: x = 4, y = 2, z = 1.

Дата добавления: 2014-12-27