Теорема о разложении определителя по элементам строки или столбца

Теорема. Определитель равен сумме произведенийэлемен­тов любой строки или столбца определителя на их алгебраические дополнения:

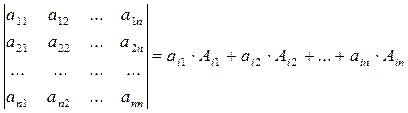Рассмотрим разложение определителя по i -й строке:

Разложение определителя no j -му столбцу:

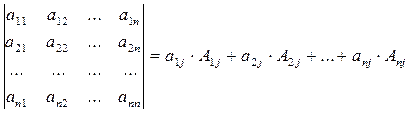Данная теорема позволяет вычислять определитель по любой строке или по любому столбцу. Важно помнить, что, вычисляя определитель разными способами, ответ должен быть одним и тем же. В качестве ряда, по которому будет раскрываться определитель, целесообразно выбирать ряд, содержащий большее количество нулей.

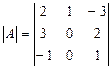
Пример 2.8. Вычислите определитель:

а) по первой строке;

б) по второму столбцу.

Решение:

Раскроем определитель по первой строке:

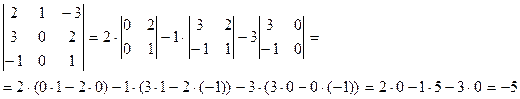
Разложим определитель по второму столбцу:

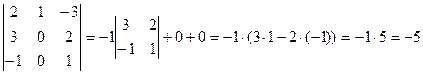
При разложении определителя по первой строке и второму столбцу получили одинаковые значения: | A | = -5.

Ответ: | A | = -5.

Теорема о разложении определителя по элементам строки или столбца позволяет вычислять определители более высоких порядков (п) сведением их к определителям более низких порядков (п-1).

Пример 2.9. Вычислите определитель четвертого порядка

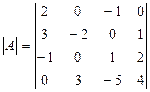
Решение: Раскроем определить по первой строке:

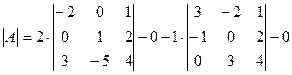
Вычислим каждый из определителей третьего порядка отдельно:

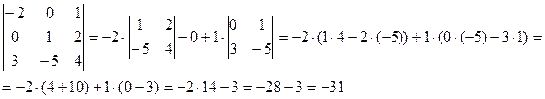
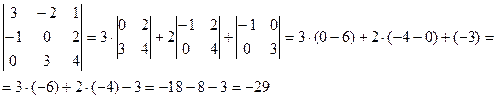
Получим, что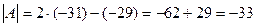

Ответ: | A | = -33.

1. Расчет определителей в электронных таблицах Microsoft Excel.

Для расчета определителя в электронных таблицах Microsoft Excel необходимо:

1. Ввести данные в ячейки электронных таблиц.

2. В любой свободной ячейке выбрать пункт меню «Вставка», раздел «функция», категорию «математические», функцию «МОПРЕД».

3. В открывшемся диалоговом окне выделить диапазон ячеек, в которых содержатся исходные данные, и нажать кнопку «ОК».

4. В ячейке, в которую была введена формула, будет содержаться значение определителя.

Пример 2.10. С помощью электронных таблиц Microsoft Excel вычислите определитель: .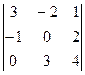

Решение.

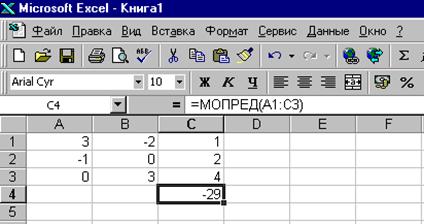
1. Введем данные в ячейки А1:С3 электронных таблиц.

2. В ячейке С4 выберем пункт меню «Вставка», раздел «функция», категорию «математические», функцию «МОПРЕД».

3. В открывшемся диалоговом окне выделим диапазон ячеек А1:С3 и нажмем кнопку «ОК».

В ячейке С4 содержится значение определителя. Он равен (–29).

Контрольные вопросы:

1. Что называется определителем матрицы?

2. Существует ли определитель матрицы размером 2х3?

3. Какие существуют свойства определителей?

4. Что называется минором элемента а_ij?

5. Чем минор элемента а_ij отличается от его алгебраического дополнения? Могут ли они иметь одинаковые числовые значения?

6. Как разложить определитель по элементам столбца или строки?

7. Как вычислить определитель с помощью электронных таблиц Microsoft Excel?

Дата добавления: 2014-12-27