Средняя геометрическая простая (невзвешенная)

Средняя гармоническая взвешенная.

Расчет средней арифметической по способу моментов

.

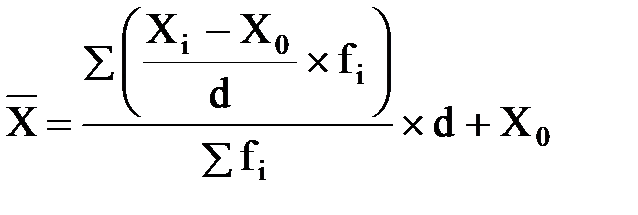Основан на свойствах средней арифметической. В качестве условного ноля - X₀ - выбирают середину одного из центральных интервалов, обладающего наибольшей частотой.

Этот способ используется только в рядах с равными интервалами.

,

где W_i = X_if_i.

Используется в тех случаях, когда не известны частоты, но они входят в состав одного из известных показателей.

Применяется при расчете средних темпов изменения явления во времени.

4. Средняя хронологическая простая (невзвешенная).

.

Используется для расчета средней в моментных равноотстоящих рядах.

Наряду с рассмотренными средними рассчитываются так называемые структурные средние - мода и медиана.

Мода Мо - значение признака, повторяющееся с наибольшей частотой.

Медиана Ме - значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Мода и медиана в интервальном вариационном ряду с равными интервалами рассчитываются по формулам.

,

где f_Мо - частота модального интервала;

f_Мо-1 - частота интервала, предшествующего модальному;

f_Мо+1 - частота интервала, следующего за модальным;

d - величина модального интервала;

X _Мо - нижняя граница модального интервала.

Модальный интервал - это интервал, имеющий наибольшую частоту.

,

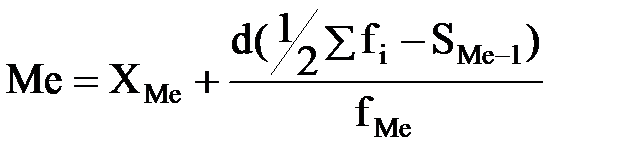где d - величина медианного интервала;

åf_i - сумма всех частот;

S_Ме-1 - накопленная частота интервала, предшествующего медианному;

f_Ме - частота медианного интервала;

X _Ме - нижняя граница медианного интервала.

Медианныминтервалом называется первый интервал, накопленная частота которого больше или равна половине суммы всех частот.

S_Ме ≥ 0,5 åf_i

Дата добавления: 2014-12-24