Тема 6. Средние величины

Средней величиной называется обобщенный количественный показатель характерного, типичного уровня массовых однородных явлений, который складывается под воздействием общих причин и условий развития.

Условные обозначения: 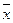— среднее значение исследуемого признака; 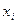- каждое индивидуальное значение усредняемого признака; 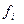- частота повторений (вес) индивидуального признака; 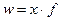– объем значений признака; n – количество единиц исследуемого признака.

Способы расчета средних: простая применяется по первичным (не сгруппированным) данным, взвешенная применяется по сгруппированным данным (известен показатель частоты).

Основное условие для правильного исчисления средней величины признака – это четкое определение исходного соотношения средней:

.

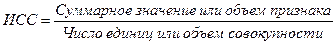Методы расчета средних:

1. Средняя арифметическая - применяется тогда, когда известны индивидуальные значения признака (х) и их количество в совокупности.

а) простая: 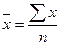; б) взвешенная: .

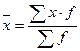2. Средняя гармоническая - применяется тогда, когда известны данные об общем объеме признака (если взвешенная – w) и индивидуальные значения признака (х), неизвестной является - частота (f).

а) простая: 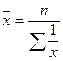; б) взвешенная: .

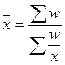3. Средняя квадратичная - используется для определения показателей вариации (колебания) признака — дисперсии и среднего квадратического отклонения.

а) простая: 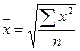; б) взвешенная: .

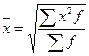4. Средняя геометрическая применяется, когда объем совокупности формируется произведением индивидуальных значений признаков. Используется для вычисления среднегодовых темпов роста: .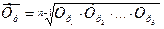

5. Средняя хронологическая применяется для определения среднего моментного уровня ряда динамики (равностоящего) .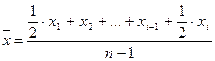

6. Структурные средние: мода (Мо) — это значение признака, которое чаще всего повторяется в ряду распределения; медиана (Мe) – значение признака, которое делит ранжированный ряд на две равные по объему части. Для интервальных рядов, структурные средние определяются по формуле:

а) 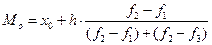, где 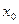- нижняя граница модального интервала; 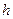- ширина модального интервала; 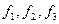- частота соответственно предмодального, модального, послемодального интервалов;

б) 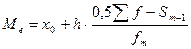, где 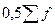- половина суммы частот; 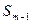- сумма накопленных частот перед медианным интервалом.

Графически структурные средние в интервальном ряду распределения определяются по гистограмме и кумуляте.

Мода - выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения (рис. 2).

Медиана - рассчитывается по кумуляте (рис. 3). Для её определения из точки на шкале накопленных частот (частностей), соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

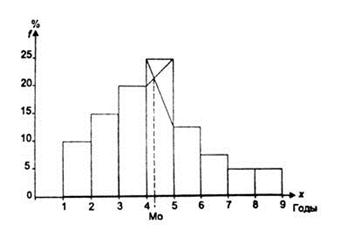
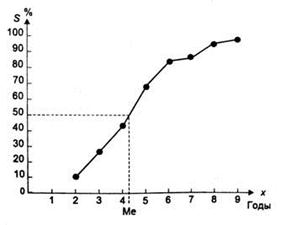
Рис. 2. Определение моды. Рис. 3. Определение медианы.

Дата добавления: 2014-12-24