Пример 1.5. На какую высоту и за какое время поднимется тело весом , брошенное вертикально вверх со скоростью

На какую высоту 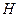и за какое время 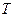поднимется тело весом 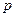, брошенное вертикально вверх со скоростью 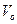, если сопротивление воздуха может быть выражено формулой 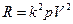, где 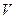— скорость тела?

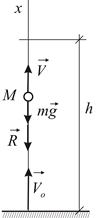
Направим ось 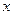вертикально вверх, полагая 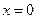на поверхности Земли (Рис.1.4). Дифференциальное уравнение движения имеет вид:

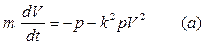
или, учитывая что 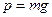, вид:

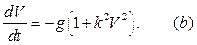
Рис.1.4

Уравнение 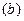представляет собой обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Чтобы получить зависимость скорости от времени, выполняем интегрирование с переменным верхним пределом. Учитывая начальные условия, получаем:

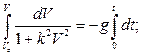
отсюда:

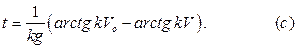
Теперь мы имеем возможность определить время подъема тела на максимальную высоту. Подставляя в уравнение (с) условия

при получаем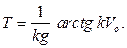

Остается определить максимальную высоту подъема 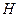. Уравнение 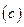можно рассматривать как дифференциальное уравнение относительно функции , поскольку 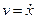, но интегрирование уравнения

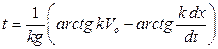
представляется неудобным.

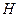Помимо зависимости , для определения нас вполне устраивает зависимость 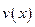, поскольку скорость в верхней точке известна: 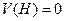. Перейдем в уравнении 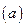от производной по 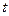к производной по 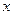, полагая

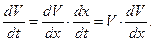
Уравнение 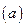принимает вид:

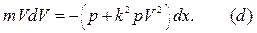
Интегрируя уравнение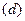

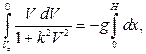получаем: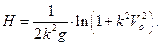

Заметим, что соотношение 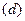представляет собой одну из форм записи теоремы об изменении кинетической энергии, которую мы докажем позднее.

Дата добавления: 2014-12-25