Пример 3.5

Диск радиуса 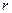вращается вокруг неподвижной оси 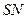с постоянной угловой скоростью 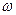. По ободу диска движется точка 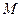, имея относительно диска постоянную по модулю скорость 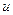. Определить абсолютную скорость и абсолютное ускорение точки .

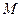Подвижную систему отсчета связываем с диском (Рис. 3.8). По отношению к диску, т.е. в относительном движении, точка 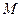движется равномерно со скоростью 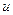, описывая окружность радиуса 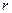с центром в точке 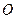. Определяем относительное ускорение точки:

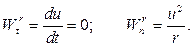
Рассмотрим переносное движение – его совершает диск. Точка 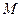диска описывает окружность с центром , плоскость которой параллельна координатной плоскости . Переносная скорость

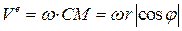
направлена по касательной к этой окружности в сторону вращения диска, т.е. перпендикулярно плоскости диска в отрицательном направлении координатной оси 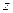. Поскольку вращение диска по условию равномерное, отличным от нуля оказывается только осестремительное ускорение:

Вектор ускорения Кориолиса точки 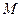направлен перпендикулярно плоскости чертежа, в которой расположены векторы и , причем, в ту сторону, откуда кратчайшее совмещение направления вектора с направлением вектора видно против хода часовой стрелки. В указанном на Рис. 3.9 положении точки 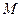вектор ускорения Кориолиса направлен на нас, т.е. параллелен координатной оси 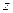в положительную сторону этой оси. На Рис. 3.9 это направление условно обозначено острием стрелки, заключенным в кружок. Модуль ускорения Кориолиса вычисляется по формуле:

.

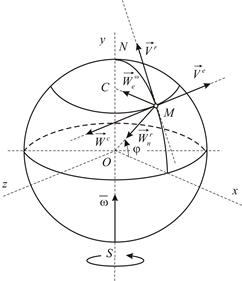
Рис.3.8		Рис.3.9

При перемещении точки 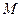по диску направление ускорения Кориолиса не будет изменяться до тех пор, пока 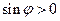, т.е. пока (точка ). При пересечении точкой 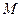координатной оси 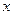ускорение Кориолиса обращается в нуль. При движении точки в нижней части диска, т.е. при 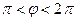, проекция ускорения Кориолиса на направление оси 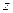становится отрицательной и вектор 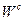направлен от нас (точк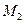и и ).

Таким образом,

Используя теорему сложения скоростей

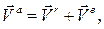
находим проекции вектора абсолютной скорости на оси подвижной системы координат:

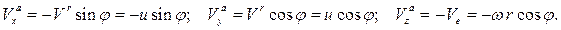
Используя теорему Кориолиса

находим проекции абсолютного ускорения точки на оси подвижной системы координат:

Примечание.

Последняя задача позволяет проиллюстрировать некоторые явления, связанные с вращением Земли, в частности, размыв берегов рек. Как видно, вращение Земли приводит к возникновению у частиц воды кориолисова ускорения, направленного перпендикулярно линии берегов. Наличие такого ускорения приводит к тому, что в северном полушарии дополнительно подмывается правый берег, который на прямолинейных участках рек заметно выше левого берега. В южном полушарии более высокий левый берег. Это явление в географии отражено в законе Бэра.

ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:

Из сборника задач И.В.Мещерского: 22.10; 22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19; 23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.

Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА - теория и практика»: комплекты СР-23;

СР-24; СР-25.

КОНТРОЛЬНЫЕ МЕРОПРИЯТИЯ:

1. После практического занятия №7(15) проводится тест «МОДУЛЬ КБ».

ЛИТЕРАТУРА:

1. Антонов В.И., Белов В.А., Егорычев О.О., Степанов Р.Н. //Курс теоретической механики (теория и практика) – М.: Архитектура – С, 2011 г.
2. Мещерский И.В.// Сборник задач по теоретической механике. – Спб.: Лань, 2010 г.

Дата добавления: 2014-12-25